
【题目】下列四种说法中,
①命题“存在x∈R,x2﹣x>0”的否定是“对于任意x∈R,x2﹣x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2, ![]() ),则f(4)的值等于
),则f(4)的值等于 ![]() ;
;
④已知向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(2,1),则向量
=(2,1),则向量 ![]() 在向量
在向量 ![]() 方向上的投影是
方向上的投影是 ![]() .
.
说法错误的个数是( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:①命题“存在x∈R,x2﹣x>0”的否定是“对于任意x∈R,x2﹣x≤0”,故①不正确;②命题“p且q为真”,则命题p、q均为真,所以“p或q为真”.反之“p或q为真”,则p、q不见得都真,所以不一定有“p且q为真”所以命题“p且q为真”是“p或q为真”的充分不必要条件,故命题②不正确;③由幂函数f(x)=xα的图象经过点(2, ![]() ),所以2α=
),所以2α= ![]() ,所以α=﹣
,所以α=﹣ ![]() ,所以幂函数为f(x)=
,所以幂函数为f(x)= ![]() ,所以f(4)=
,所以f(4)= ![]() ,所以命题③正确;④∵向量
,所以命题③正确;④∵向量 ![]() =(3,﹣4),
=(3,﹣4), ![]() =(2,1),∴
=(2,1),∴ ![]()
![]() =3×2+(﹣4)×1=2,|
=3×2+(﹣4)×1=2,| ![]() |=
|= ![]() ,∴向量
,∴向量 ![]() 在向量
在向量 ![]() 的方向上的投影为:
的方向上的投影为: ![]() =
= ![]() ,故④不正确.故选:C.
,故④不正确.故选:C.
命题①是考查特称命题的否定,特称命题的否定是全称命题;
命题②先由“p且q为真”推出p、q的真假,然后判断“p或q”的真假,反之再加以判断;
命题③直接把点的坐标代入幂函数求出α,然后在幂函数解析式中取x=4求值;
命题④向量 ![]() 在向量
在向量 ![]() 的方向上的投影为:
的方向上的投影为: ![]() ,即可得出结论.
,即可得出结论.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】若F1 , F2是椭圆C: ![]() +
+ ![]() =1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M. (Ⅰ)求椭圆C的方程;
=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M. (Ⅰ)求椭圆C的方程;
(Ⅱ)过点(0, ![]() )的直线l与椭圆C交于两点A、B,线段AB的中垂线l1交x轴于点N,R是线段AN的中点,求直线l1与直线BR的交点E的轨迹方程.
)的直线l与椭圆C交于两点A、B,线段AB的中垂线l1交x轴于点N,R是线段AN的中点,求直线l1与直线BR的交点E的轨迹方程.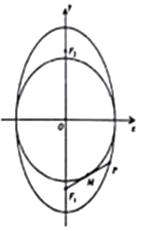
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“x2+x﹣2>0”是“x>1”的充分不必要条件
B.“若am2<bm2 , 则a<b”的逆否命题为真命题
C.命题“?x∈R,使得2x2﹣1<0”的否定是“?x∈R,均有2x2﹣1>0”
D.命题“若x= ![]() ,则tanx=1”的逆命题为真命题
,则tanx=1”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且Sn= ![]() nan+an﹣c(c是常数,n∈N*),a2=6.
nan+an﹣c(c是常数,n∈N*),a2=6.
(Ⅰ)求c的值及数列{an}的通项公式;
(Ⅱ)设bn= ![]() ,数列{bn}的前n项和为Tn , 若2Tn>m﹣2对n∈N*恒成立,求最大正整数m的值.
,数列{bn}的前n项和为Tn , 若2Tn>m﹣2对n∈N*恒成立,求最大正整数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,面积S= ![]() abcosC
abcosC
(1)求角C的大小;
(2)设函数f(x)= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]() ,求f(B)的最大值,及取得最大值时角B的值.
,求f(B)的最大值,及取得最大值时角B的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:f1(x)=f(x),当n≥2且x∈N*时,fn(x)=f(fn﹣1(x)),对于函数f(x)定义域内的x0 , 若正在正整数n是使得fn(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是(写出所有正确命题的编号)
①1是f(x)的一个3~周期点;
②3是点 ![]() 的最小正周期;
的最小正周期;
③对于任意正整数n,都有fn( ![]() )=
)= ![]() ;
;
④若x0∈( ![]() ,1],则x0是f(x)的一个2~周期点.
,1],则x0是f(x)的一个2~周期点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区超市购进了A,B,C,D四种新产品,为了解新产品的销售情况,该超市随机调查了15位顾客(记为ai , i=1,2,3,…,15)购买这四种新产品的情况,记录如下(单位:件):
顾 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 |
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
(Ⅰ)若该超市每天的客流量约为300人次,一个月按30天计算,试估计产品A的月销售量(单位:件);
(Ⅱ)为推广新产品,超市向购买两种以上(含两种)新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物,记他们获得的电子红包的总金额为X,求随机变量X的分布列和数学期望;
(Ⅲ)若某顾客已选中产品B,为提高超市销售业绩,应该向其推荐哪种新产品?(结果不需要证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com