
【题目】已知椭圆的中心在原点,焦点在x轴上,长轴的两个端点分别为![]() 、
、![]() .短轴的两个端点分别为
.短轴的两个端点分别为![]() ,
,![]() .菱形
.菱形![]() 的面积为
的面积为![]() ,离心率
,离心率![]() .
.
(1)求椭圆的标准方程;
(2)设![]() ,经过点M作斜率不为0的直线
,经过点M作斜率不为0的直线![]() 交椭圆C于A、B两点,若
交椭圆C于A、B两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)由已知条件得出关于![]() 方程组求解即可;
方程组求解即可;
(2)方法一:先由已知得出![]() 中垂线过
中垂线过![]() 点,设出直线
点,设出直线![]() 的方程,
的方程,![]() 点坐标,联立直线方程和椭圆方程,消去
点坐标,联立直线方程和椭圆方程,消去![]() 得关于
得关于![]() 的一元二次方程,利用韦达定理得出
的一元二次方程,利用韦达定理得出![]() 点坐标关系,最后利用
点坐标关系,最后利用![]() 中点在中垂线上得到关系式求解即可.方法二:先设出直线
中点在中垂线上得到关系式求解即可.方法二:先设出直线![]() 的方程,
的方程,![]() 点坐标,由已知向量关系式化简为坐标关系,利用点差法得出
点坐标,由已知向量关系式化简为坐标关系,利用点差法得出![]() 点坐标关系,然后把直线
点坐标关系,然后把直线![]() 方程与椭圆方程联立得关于
方程与椭圆方程联立得关于![]() 的一元二次方程,利用韦达定理即可得到等量关系,求解即可.
的一元二次方程,利用韦达定理即可得到等量关系,求解即可.
解:(1)∵![]() ,∴
,∴![]() .
.
又因为菱形![]() 的面积为
的面积为![]() ,即有
,即有![]() ,即
,即![]() ,
,
所以![]() ,从而
,从而![]() ,
,
所以椭圆C的标准方程为![]() .
.
(2)由![]() ,知
,知![]() ,设
,设![]() ,由向量加法的意义,知
,由向量加法的意义,知![]() 是线段
是线段![]() 的中垂线,设直线
的中垂线,设直线![]() 的方程为
的方程为![]() ,经过N且与
,经过N且与![]() 垂直的直线为
垂直的直线为![]() .
.
设![]() ,由
,由![]() 消去
消去![]() ,得
,得![]() ,
,
于是有![]() .
.
关于A,B关于直线![]() 对称,故点
对称,故点![]() 必在此直线上,
必在此直线上,
所以![]() ,即
,即![]() ,所以
,所以![]() 或
或![]() ,
,
故所求的直线![]() 的方程为
的方程为![]() 或
或![]() ,即
,即![]() 或
或![]() .
.
解法二:设![]() ,因为
,因为![]() ,所以
,所以
![]() .
.
由题得![]() ,即
,即
![]() .①
.①
因为A、B在椭圆C上,所以![]() ,所以
,所以![]() .两式相减,得
.两式相减,得![]() ,② 因为
,② 因为![]() 的斜率不为0,所以
的斜率不为0,所以![]() ,将②代①,得
,将②代①,得![]() .③
.③
因直线![]() 经过
经过![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 消去
消去![]() ,得
,得![]() ,
,
于是有![]() ,代入③得
,代入③得![]() ,解得
,解得![]() ,或
,或![]() .
.
故所求直线![]() 的方程为
的方程为![]() 或
或![]() ,即
,即![]() .或
.或![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的菱形,∠DAB=60°,AD⊥PD,点F为棱PD的中点.
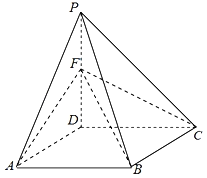
(1)在棱BC上是否存在一点E,使得CF∥平面PAE,并说明理由;
(2)若AC⊥PB,二面角D﹣FC﹣B的余弦值为![]() 时,求直线AF与平面BCF所成的角的正弦值.
时,求直线AF与平面BCF所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥S一ABC中,△ABC与△SBC都是边长为1的正三角形,二面角A﹣BC﹣S的大小为![]() ,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
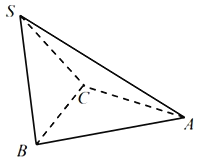
A.![]() πB.
πB.![]() πC.
πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,组合体由半个圆锥![]() 和一个三棱锥
和一个三棱锥![]() 构成,其中
构成,其中![]() 是圆锥
是圆锥![]() 底面圆心,
底面圆心,![]() 是圆弧
是圆弧![]() 上一点,满足
上一点,满足![]() 是锐角,
是锐角,![]() .
.
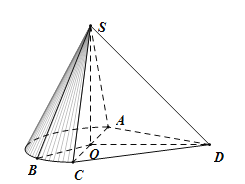
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明;
,并写出作图步骤,但不要求证明;
(2)在(1)中,若![]() 是
是![]() 中点,且
中点,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某次考试之后,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学、物理成绩(单位:分)对应如下表,对应散点图如图所示:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学成绩 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理成绩 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
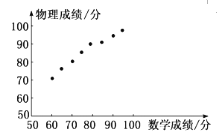
根据以上信息,则下列结论:
①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则可以判断出甲同学的物理成绩一定比乙同学的物理成绩高;
④从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则不能判断出甲同学的物理成绩一定比乙同学的物理成绩高;
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎期间某商场开通三种平台销售商品,收集一月内的数据如图1;为了解消费者对各平台销售方式的满意程度,该商场用分层抽样的方法抽取4%的顾客进行满意度调查,得到的数据如图2.下列说法错误的是( )
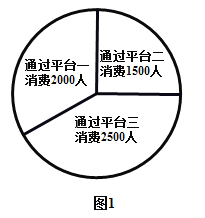
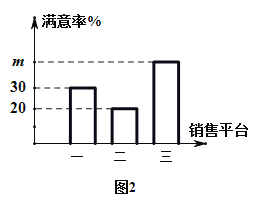
A.样本容量为240
B.若样本中对平台三满意的人数为40,则![]()
C.总体中对平台二满意的消费者人数约为300
D.样本中对平台一满意的人数为24人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4-4:坐标系与参数方程)
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是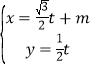 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com