
数列{an}的前n项和记为Sn,a1=1,an+1=2Sn+1(n≥1,n∈N*),则数列{an}的通项公式是_______.
an=3n-1
【解析】【思路点拨】根据an和Sn的关系转换an+1=2Sn+1(n≥1)为an+1与an的关系或者Sn+1与Sn的关系.
解:方法一:由an+1=2Sn+1可得an=2Sn-1+1(n≥2),两式相减得an+1-an=2an,an+1=3an(n≥2).
又a2=2S1+1=3,
∴a2=3a1,故{an}是首项为1,公比为3的等比数列,
∴an=3n-1.
方法二:由于an+1=Sn+1-Sn,
an+1=2Sn+1,
所以Sn+1-Sn=2Sn+1,Sn+1=3Sn+1,
把这个关系化为Sn+1+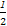 =3(Sn+
=3(Sn+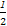 ),
),
即得数列{Sn+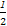 }为首项是S1+
}为首项是S1+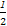 =
=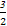 ,
,
公比是3的等比数列,故Sn+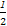 =
=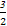 ×3n-1=
×3n-1=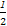 ×3n,
×3n,
故Sn=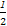 ×3n-
×3n-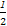 .
.
所以,当n≥2时,an=Sn-Sn-1=3n-1,
由n=1时a1=1也适合这个公式,知所求的数列{an}的通项公式是an=3n-1.
【方法技巧】an和Sn关系的应用技巧
在根据数列的通项an与前n项和的关系求解数列的通项公式时,要考虑两个方面,一个是根据Sn+1-Sn=an+1把数列中的和转化为数列的通项之间的关系;一个是根据an+1=Sn+1-Sn把数列中的通项转化为前n项和的关系,先求Sn再求an.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十二第三章第六节练习卷(解析版) 题型:选择题
函数y= sin2x+
sin2x+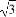 cos2x-
cos2x-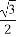 的最小正周期等于( )
的最小正周期等于( )
(A)π (B)2π (C) (D)
(D)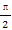
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十七第四章第三节练习卷(解析版) 题型:选择题
设a,b是不共线的两个向量,其夹角是θ,若函数f(x)=(xa+b)·(a-xb)(x∈R)在(0,+∞)上有最大值,则( )
(A)|a|<|b|,且θ是钝角
(B)|a|<|b|,且θ是锐角
(C)|a|>|b|,且θ是钝角
(D)|a|>|b|,且θ是锐角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十一第三章第五节练习卷(解析版) 题型:选择题
已知向量a=(sin(α+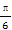 ),1),b=(4,4cosα-
),1),b=(4,4cosα-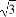 ),若a⊥b,则sin(α+
),若a⊥b,则sin(α+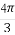 )=( )
)=( )
(A)-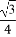 (B)-
(B)- (C)
(C)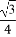 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷(解析版) 题型:解答题
已知数列{an}的前n项和为Sn,若S1=1,S2=2,且Sn+1-3Sn+2Sn-1=0(n∈N*且n≥2),求该数列的通项公式.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十第五章第一节练习卷(解析版) 题型:选择题
在数列{an}中,a1=1,anan-1=an-1+(-1)n(n≥2,n∈N*),则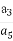 的值是( )
的值是( )
(A)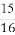 (B)
(B)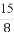 (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷(解析版) 题型:解答题
设函数f(x)= +sinx的所有正的极小值点从小到大排成的数列为{xn}.
+sinx的所有正的极小值点从小到大排成的数列为{xn}.
(1)求数列{xn}的通项公式.
(2)设{xn}的前n项和为Sn,求sinSn.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:填空题
已知集合A={x∈R||x+2|<3},B={x∈R|(x-m)(x-2)<0},且A∩B=(-1,n),则m= ,n= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十五第六章第一节练习卷(解析版) 题型:选择题
已知a,b为实数,则“a>b>1”是“ <
< ”的( )
”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com