
| A. | [2,+∞]∪(-∞,$\frac{1}{2}$] | B. | (0,$\frac{1}{2}$]∪[2,+∞) | C. | [$\frac{1}{2}$,2] | D. | (0,$\frac{1}{2}$] |
分析 由偶函数的性质将f(log2a)+f(log${\;}_{\frac{1}{2}}$a)≤2f(-1),化为:f(log2a)≤f(1),再由f(x)的单调性列出不等式,根据对数函数的性质求出a的取值范围.
解答 解:因为函数f(x)是定义在R上的偶函数,
所以f(log${\;}_{\frac{1}{2}}$a)=f(-log2a)=f(log2a),
则f(log2a)+f(log${\;}_{\frac{1}{2}}$a)≤2f(-1),为:f(log2a)≤f(1),
因为函数f(x)在区间[0,+∞)上单调递减,
所以|log2a|≥1,解得0<a≤$\frac{1}{2}$或a≥2,
则a的取值范围是(0,$\frac{1}{2}$]∪[2,+∞)
故选:B.
点评 本题考查函数的奇偶性、单调性的应用,以及对数函数的性质,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{4}$,$\frac{π}{4}$] | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [-$\frac{π}{3}$,$\frac{π}{6}$] | D. | [$\frac{π}{6}$,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在三角形中,若A>B,则sinA>sinB | |
| B. | 若等比数列的前n项和Sn=2n+k,则必有k=-1 | |
| C. | A,B为两个定点,k为非零常数,|$\overrightarrow{PA}|-|\overrightarrow{PB}$|=k,则动点P的轨迹为双曲线 | |
| D. | 曲线$\frac{x^2}{16}-\frac{y^2}{9}$=1与曲线$\frac{x^2}{35-λ}+\frac{y^2}{10-λ}$=1(λ<10)有相同的焦点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x+1)=(x+1)2+$\frac{1}{(x+1)^{2}}$ | B. | f(x+1)=(x-$\frac{1}{x}$)2+$\frac{1}{(x-\frac{1}{x})^{2}}$ | ||
| C. | f(x+1)=(x+1)2+2 | D. | f(x+1)=(x+1)2+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
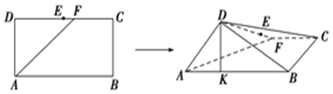 如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{3}}{2}$,2) | D. | ($\frac{\sqrt{3}}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 165° | B. | 60° | C. | 25° | D. | 15° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosθ<tanθ<sinθ | B. | sinθ<cosθ<tanθ | C. | tanθ<sinθ<cosθ | D. | cosθ<sinθ<tanθ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com