分析:(1)利用条件得PF1⊥PF2以及PF1|2+|PF2|2=(2c)2=16m2.再利用椭圆定义求出关于m的方程,解出m的值就可求椭圆C的左,右焦点F1、F2.
(2)把已知条件转化为|QF1|2=2(|QF2|2-1),整理即可求出动点Q的轨迹方程.
解答:解:(1)∵c
2=a
2-b
2,∴c
2=4m
2.(2分)
又∵
•=0∴PF
1⊥PF
2,(3分)
∴|PF
1|
2+|PF
2|
2=(2c)
2=16m
2.(5分)
由椭圆定义可知
|PF1|+|PF2|=2a=2m,(|PF
1|+|PF
2|)
2=16m
2+16=24m
2,(6分)
从而得m
2=2,c
2=4m
2=8,c=2
.∴F
1(-2
,0)、F
2(2
,0).(7分)
(2)∵F
1(-2
,0),F
2(2
,0),
由已知:
|QF1|=|QM|,即|QF
1|
2=2|QM|
2,
所以有:|QF
1|
2=2(|QF
2|
2-1),设点Q(x,y),(9分)
则(x+2
)
2+y
2=2[(x-2
)
2+y
2-1],(12分)
即(x-6
)
2+y
2=66)
综上所述,所求轨迹方程为:(x-6
)
2+y
2=66.(14分)
点评:本题涉及到求动点的轨迹方程问题.在求动点的轨迹方程时,一般是利用条件得到关于动点的等式整理就可求出对应动点的轨迹方程.

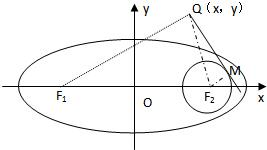 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C:

 设F1、F2分别是椭圆C:
设F1、F2分别是椭圆C: