
ЁОЬтФПЁПЬяМЩКЭЦыЭѕШќТэЪЧРњЪЗЩЯгаУћЕФЙЪЪТЃЌЩшЦыЭѕЕФШ§ЦЅТэЗжБ№ЮЊ![]() ЃЌЬяМЩЕФШ§ЦЅТэЗжБ№ЮЊ
ЃЌЬяМЩЕФШ§ЦЅТэЗжБ№ЮЊ![]() .Ш§ЦЅТэИїБШШќвЛДЮЃЌЪЄСНГЁепЮЊЛёЪЄ.ШєетСљЦЅТэБШШќЕФгХСгГЬЖШПЩвдгУвдЯТВЛЕШЪНБэЪОЃК
.Ш§ЦЅТэИїБШШќвЛДЮЃЌЪЄСНГЁепЮЊЛёЪЄ.ШєетСљЦЅТэБШШќЕФгХСгГЬЖШПЩвдгУвдЯТВЛЕШЪНБэЪОЃК ![]() .
.
ЃЈ1ЃЉШчЙћЫЋЗНОљВЛжЊЕРЖдЗНТэЕФГіГЁЫГађЃЌЧѓЬяМЩЛёЪЄЕФИХТЪЃЛ
ЃЈ2ЃЉЮЊСЫЕУЕНИќДѓЕФЛёЪЄИХТЪЃЌЬяМЩдЄЯШХЩГіЬНзгЕНЦыЭѕДІДђЬНЪЕЧщЃЌЕУжЊЦыЭѕЕквЛГЁБиГіЩЯЕШТэЃЌФЧУДЃЌЬяМЩгІдѕбљАВХХГіТэЕФЫГађЃЌВХФмЪЙздМКЛёЪЄЕФИХТЪзюДѓЃПзюДѓИХТЪЪЧЖрЩйЃП
ЁОД№АИЁП(1) ![]() ЃЈ2ЃЉЬяМЩАД
ЃЈ2ЃЉЬяМЩАД![]() Лђ
Лђ![]() ЕФЫГађГіТэЃЌВХФмЪЙздМКЛёЪЄЕФИХТЪДяЕНзюДѓ
ЕФЫГађГіТэЃЌВХФмЪЙздМКЛёЪЄЕФИХТЪДяЕНзюДѓ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЦыЭѕгыЬяМЩШќТэЃЌгаСљжжЧщПіЃЌЬяМЩЛёЪЄЕФжЛгавЛжжЃЌЙЪЬяМЩЛёЪЄЕФЃТЪЮЊ![]() .ЃЈ2ЃЉвђЦыЭѕЕквЛГЁБиГіЩЯЕШТэ
.ЃЈ2ЃЉвђЦыЭѕЕквЛГЁБиГіЩЯЕШТэ![]() ЃЌШєЬяМЩЕквЛГЁБиГіЩЯЕШТэ
ЃЌШєЬяМЩЕквЛГЁБиГіЩЯЕШТэ![]() ЛђжаЕШТэ
ЛђжаЕШТэ![]() ЃЌдђЪЃЯТЖўГЁЃЌЬяМЩжСЩйЪфвЛГЁЃЌетЪБЬяМЩБиАм.ЮЊСЫЪЙздМКЛёЪЄЕФИХТЪзюДѓЃЌЬяМЩЕквЛГЁгІГіЯТЕШТэ
ЃЌдђЪЃЯТЖўГЁЃЌЬяМЩжСЩйЪфвЛГЁЃЌетЪБЬяМЩБиАм.ЮЊСЫЪЙздМКЛёЪЄЕФИХТЪзюДѓЃЌЬяМЩЕквЛГЁгІГіЯТЕШТэ![]() ЃЌдкгрЯТЕФСНГЁБШШќжаЃЌЬяМЩЛёЪЄЕФИХТЪЮЊ
ЃЌдкгрЯТЕФСНГЁБШШќжаЃЌЬяМЩЛёЪЄЕФИХТЪЮЊ![]() ЃЈгрЯТСНГЁЪЧЦыЭѕЕФжаТэЖдЬяМЩЩЯТэКЭЦыЭѕЕФЯТТэЖдЬяМЩЕФЩЯТэЃЛЦыЭѕЕФжаТэЖдЬяМЩЯТТэКЭЦыЭѕЕФЯТТэЖдЬяМЩЕФжаТэЃЌЧАепЬяМЩгЎЃЌКѓепЬяМЩЪфЃЉ
ЃЈгрЯТСНГЁЪЧЦыЭѕЕФжаТэЖдЬяМЩЩЯТэКЭЦыЭѕЕФЯТТэЖдЬяМЩЕФЩЯТэЃЛЦыЭѕЕФжаТэЖдЬяМЩЯТТэКЭЦыЭѕЕФЯТТэЖдЬяМЩЕФжаТэЃЌЧАепЬяМЩгЎЃЌКѓепЬяМЩЪфЃЉ
НтЮіЃКМЧ![]() гы
гы![]() БШШќЮЊ
БШШќЮЊ![]() ЃЌЦфЫќЭЌРэ.
ЃЌЦфЫќЭЌРэ.
ЃЈ1ЃЉЦыЭѕгыЬяМЩШќТэЃЌгаШчЯТСљжжЧщПіЃК
![]() ЃЛ
ЃЛ ![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ ![]() ЃЛ
ЃЛ
![]() ЃЛ
ЃЛ ![]() ЃЛ
ЃЛ
ЦфжаЬяМЩЛёЪЄЕФжЛгавЛжжЃК ![]() .ЙЪЬяМЩЛёЪЄЕФЃТЪЮЊ
.ЙЪЬяМЩЛёЪЄЕФЃТЪЮЊ![]() .
.
ЃЈ2ЃЉвбжЊЦыЭѕЕквЛГЁБиГіЩЯЕШТэ![]() ЃЌШєЬяМЩЕквЛГЁБиГіЩЯЕШТэ
ЃЌШєЬяМЩЕквЛГЁБиГіЩЯЕШТэ![]() ЛђжаЕШТэ
ЛђжаЕШТэ![]() ЃЌдђЪЃЯТЖўГЁЃЌЬяМЩжСЩйЪфвЛГЁЃЌетЪБЬяМЩБиАм.ЮЊСЫЪЙздМКЛёЪЄЕФИХТЪзюДѓЃЌЬяМЩЕквЛГЁгІГіЯТЕШТэ
ЃЌдђЪЃЯТЖўГЁЃЌЬяМЩжСЩйЪфвЛГЁЃЌетЪБЬяМЩБиАм.ЮЊСЫЪЙздМКЛёЪЄЕФИХТЪзюДѓЃЌЬяМЩЕквЛГЁгІГіЯТЕШТэ![]() ЃЌКѓСНГЁгаСНжжЧщаЮЃК
ЃЌКѓСНГЁгаСНжжЧщаЮЃК
ЂйШєЦыЭѕЕкЖўГЁХЩГіжаЕШТэ![]() ЃЌПЩФмЕФЖдеѓЮЊЃК
ЃЌПЩФмЕФЖдеѓЮЊЃК ![]() Лђ
Лђ![]() .ЬяМЩЛёЪЄЕФИХТЪЮЊ
.ЬяМЩЛёЪЄЕФИХТЪЮЊ![]() ЃЌ
ЃЌ
ЂкШєЦыЭѕЕкЖўГЁХЩГіЯТЕШТэ![]() ЃЌПЩФмЕФЖдеѓЮЊЃК
ЃЌПЩФмЕФЖдеѓЮЊЃК ![]() Лђ
Лђ![]() .ЬяМЩЛёЪЄЕФИХТЪвВЮЊ
.ЬяМЩЛёЪЄЕФИХТЪвВЮЊ![]() .
.
ЫљвдЃЌЬяМЩАД![]() Лђ
Лђ![]() ЕФЫГађГіТэЃЌВХФмЪЙздМКЛёЪЄЕФИХТЪДяЕНзюДѓ
ЕФЫГађГіТэЃЌВХФмЪЙздМКЛёЪЄЕФИХТЪДяЕНзюДѓ![]() .
.


 ПЊаФСЗЯАПЮПЮСЗгыЕЅдЊМьВтЯЕСаД№АИ
ПЊаФСЗЯАПЮПЮСЗгыЕЅдЊМьВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯпЖЮABЕФСНИіЖЫЕуAЁЂBЗжБ№дкxжсКЭyжсЩЯЛЌЖЏЃЌЧвЈOABЈO=2ЃЎ
ЃЈ1ЃЉЧѓЯпЖЮABЕФжаЕуPЕФЙьМЃCЕФЗНГЬЃЛ
ЃЈ2ЃЉЧѓЙ§ЕуM(1ЃЌ2)ЧвКЭЙьМЃCЯрЧаЕФжБЯпЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЙ§ХзЮяЯпy2=4xЕФНЙЕуFЕФжБЯпlНЛХзЮяЯпгкЕуAЃЌBЃЌШєвдABЮЊжБОЖЕФдВЙ§ЕуPЃЈЉ1ЃЌ2ЃЉЃЌЧвгыxжсНЛгкMЃЈmЃЌ0ЃЉЃЌNЃЈnЃЌ0ЃЉСНЕуЃЌдђmn=ЃЈ ЃЉ
A.3
B.2
C.Љ3
D.Љ2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈВЛе§ШЗЕФЪЧЃЈ ЃЉ
A. ЗНГЬ![]() гаЪЕИљ
гаЪЕИљ![]() КЏЪ§
КЏЪ§![]() гаСуЕу
гаСуЕу
B. ![]() гаСНИіВЛЭЌЕФЪЕИљ
гаСНИіВЛЭЌЕФЪЕИљ
C. КЏЪ§![]() дк
дк![]() ЩЯТњзу
ЩЯТњзу![]() ЃЌдђ
ЃЌдђ![]() дк
дк![]() ФкгаСуЕу
ФкгаСуЕу
D. ЕЅЕїКЏЪ§ШєгаСуЕуЃЌжСЖргавЛИі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ{an}ЪЧЙЋВюВЛЮЊСуЕФЕШВюЪ§СаЃЌa1=1ЃЌЧвa1 ЃЌ a3 ЃЌ a9ГЩЕШБШЪ§СаЃЎ
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЃЛ
ЃЈ2ЃЉЩшЪ§Са{an}ЕФЧАnЯюКЭЮЊSn ЃЌ Сю ![]() ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTn ЃЎ
ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTn ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊМЏКЯA={1ЃЌ3ЃЌ5ЃЌ7}ЃЌB={x|ЃЈ2xЉ1ЃЉЃЈxЉ5ЃЉЃО0}ЃЌдђAЁЩЃЈRBЃЉЃЈ ЃЉ
A.{1ЃЌ3}
B.{1ЃЌ3ЃЌ5}
C.{3ЃЌ5}
D.{3ЃЌ5ЃЌ7}
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=x3+ax2+bxгаСНИіМЋжЕЕуx1ЁЂx2 ЃЌ Чвx1ЃМx2 ЃЌ Шєx1+2x0=3x2 ЃЌ КЏЪ§gЃЈxЃЉ=fЃЈxЃЉЉfЃЈx0ЃЉЃЌдђgЃЈxЃЉЃЈ ЃЉ
A.ЧЁгавЛИіСуЕу
B.ЧЁгаСНИіСуЕу
C.ЧЁгаШ§ИіСуЕу
D.жСЖрСНИіСуЕу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБЫФРтжљ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЪЧЬнаЮЃЌ
ЪЧЬнаЮЃЌ ![]() .
.
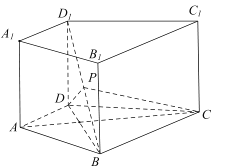
(Ђё)ЧѓжЄЃК ![]() ЃЛ
ЃЛ
(Ђђ)Шє![]() ,Еу
,Еу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЎЧыдкЯпЖЮ
ЕФжаЕуЃЎЧыдкЯпЖЮ![]() ЩЯеввЛЕу
ЩЯеввЛЕу![]() ,ЪЙ
,ЪЙ![]() ЦНУц
ЦНУц![]() ЃЌВЂЫЕУїРэгЩ.
ЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНЬхABCDЉA1B1C1D1жаЃЌEЃЌFЗжБ№ЮЊCC1КЭBB1ЕФжаЕуЃЌдђвьУцжБЯпAEгыD1FЫљГЩНЧЕФгрЯвжЕЮЊЃЈ ЃЉ
A.0
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com