练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知tan（3π-α）=-$\frac{1}{2}$，tan（β-α）=-$\frac{1}{3}$，则tan β=（　　）
    A．1B．$\frac{1}{7}$C．$\frac{5}{7}$D．$\frac{5}{9}$

    分析 利用诱导公式求得 tanα，利用两角和的正切公式求得tan β=tan[（β-α）+α]的值．

    解答 解：∵tan（3π-α）=-tanα=-$\frac{1}{2}$，∴tanα=$\frac{1}{2}$，又tan（β-α）=-$\frac{1}{3}$，
    则tan β=tan[（β-α）+α]=$\frac{tan（β-α）+tanα}{1-tan（β-α）•tanα}$=$\frac{-\frac{1}{3}+\frac{1}{2}}{1-（-\frac{1}{3}）•\frac{1}{2}}$=$\frac{1}{7}$，
    故选：B．

    点评 本题主要考查诱导公式、两角和的正切公式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    4．已知tanθ=$\frac{1}{2}$，则tan（$\frac{π}{4}$-θ）=（　　）
    A．3B．-3C．$\frac{1}{3}$D．-$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．“直线l的方程为y=k（x-2）”是“直线l经过点（2，0）”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

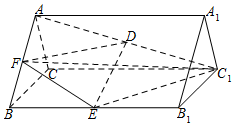    2．如图，在正三棱柱ABC-A1B1C1中，AB=2，AA1=3，D，E分别为AC1和BB1的中点．
    （Ⅰ）求证：DE∥平面ABC；
    （Ⅱ）若F为AB中点，求三棱锥F-C1DE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知命题p：函数y=3-ax+1的图象恒过定点（1，3）；命题q：若函数y=f（x-3）为偶函数，则函数y=f（x）的图象关于直线x=3对称，则下列命题为真命题的是（　　）
    A．p∨qB．p∧qC．￢p∧qD．p∨￢q

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足cos$\frac{A}{2}$=$\frac{2\sqrt{5}}{5}$，bccosA=3．
    （Ⅰ）求△ABC的面积；
    （Ⅱ）若$b+c=4\sqrt{2}$，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．在复平面内，复数z的对应点为（1，1），则z2=（　　）
    A．$\sqrt{2}$B．2iC．$-\sqrt{2}$D．.2+2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知抛物线E：y2=2px（P＞0）的准线为x=-1，M，N为直线x=-2上的两点，M，N两点的纵坐标之积为-8，P为抛物线上一动点，PN，PM，分别交抛物线于A，B两点．
    （1）求抛物线E的方程；
    （2））问直线AB是否过定点，若过定点，请求出此定点；若不过定点，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=$\left\{\begin{array}{l}{lnx，x≥1}\\{1-\frac{x}{2}，x＜1}\end{array}\right.$，若F（x）=f[f（x）+1]+m有两个零点x1，x2，则x1+x2的取值范围是（　　）
    A．[4-2ln2，+∞）B．[1+$\sqrt{e}$，+∞）C．[4-2ln2，1+$\sqrt{e}$）D．（-∞，1+$\sqrt{e}$）

    查看答案和解析>>

    同步练习册答案