
【题目】(1)![]() 为何值时,
为何值时,![]() .①有且仅有一个零点;②有两个零点且均比-1大;
.①有且仅有一个零点;②有两个零点且均比-1大;
(2)若函数![]() 有4个零点,求实数
有4个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ① m=4或m=-1;②(-5,-1);(2) (-4,0).
【解析】
试题(1)①![]() 有且仅有一个零点方程
有且仅有一个零点方程![]() 有两个相等实根Δ=0;②设f(x)的两个零点分别为
有两个相等实根Δ=0;②设f(x)的两个零点分别为![]() ,则
,则![]() =-2m,
=-2m,![]() =3m+4.由题意,知
=3m+4.由题意,知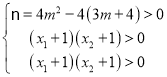 ;
;
(2)数形结合,作出g(x)=|4x-x2|和h(x)=-a的图象即可.
试题解析:
(1)①![]() 有且仅有一个零点方程
有且仅有一个零点方程![]() 有两个相等实根Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.
有两个相等实根Δ=0,即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.
②设f(x)的两个零点分别为![]() ,
,
则![]() =-2m,
=-2m,![]() =3m+4.
=3m+4.
由题意,知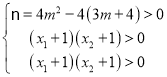
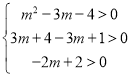
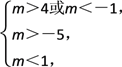
∴-5<m<-1.故m的取值范围为(-5,-1).
(2)令f(x)=0,得|4x-x2|+a=0,
则|4x-x2|=-a.
令g(x)=|4x-x2|,
h(x)=-a.
作出g(x),h(x)的图象.
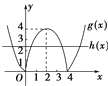
由图象可知,当0<-a<4,
即![]() 时,g(x)与h(x)的图象有4个交点.
时,g(x)与h(x)的图象有4个交点.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C0: ![]() ,动圆C1:
,动圆C1: ![]() .点A1 , A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点.
.点A1 , A2分别为C0的左右顶点,C1与C0相交于A,B,C,D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2: ![]() 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2 . 若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2 . 若矩形ABCD与矩形A′B′C′D′的面积相等,证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用二分法求函数![]() 的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
的一个正零点的近似值(精确度为0.1)时,依次计算得到如下数据:f(1)=–2,f(1.5)=0.625,f(1.25)≈–0.984,f(1.375)≈–0.260,关于下一步的说法正确的是( )
A. 已经达到精确度的要求,可以取1.4作为近似值
B. 已经达到精确度的要求,可以取1.375作为近似值
C. 没有达到精确度的要求,应该接着计算f(1.4375)
D. 没有达到精确度的要求,应该接着计算f(1.3125)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关线性回归分析的六个命题:
①线性回归直线必过样本数据的中心点![]() ;
;
②回归直线就是散点图中经过样本数据点最多的那条直线;
③当相关性系数![]() 时,两个变量正相关;
时,两个变量正相关;
④如果两个变量的相关性越强,则相关性系数![]() 就越接近于1;
就越接近于1;
⑤残差图中残差点所在的水平带状区域越宽,则回归方程的预报精确度越高;
⑥甲、乙两个模型的![]() 分别约为0.88和0.80,则模型乙的拟合效果更好.
分别约为0.88和0.80,则模型乙的拟合效果更好.
其中真命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设N=2n(n∈N* , n≥2),将N个数x1 , x2 , …,xN依次放入编号为1,2,…,N的N个位置,得到排列P0=x1x2…xN . 将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前 ![]() 和后
和后 ![]() 个位置,得到排列P1=x1x3…xN﹣1x2x4…xN , 将此操作称为C变换,将P1分成两段,每段
个位置,得到排列P1=x1x3…xN﹣1x2x4…xN , 将此操作称为C变换,将P1分成两段,每段 ![]() 个数,并对每段作C变换,得到P2 , 当2≤i≤n﹣2时,将Pi分成2i段,每段
个数,并对每段作C变换,得到P2 , 当2≤i≤n﹣2时,将Pi分成2i段,每段 ![]() 个数,并对每段作C变换,得到Pi+1 , 例如,当N=8时,P2=x1x5x3x7x2x6x4x8 , 此时x7位于P2中的第4个位置.
个数,并对每段作C变换,得到Pi+1 , 例如,当N=8时,P2=x1x5x3x7x2x6x4x8 , 此时x7位于P2中的第4个位置.
(1)当N=16时,x7位于P2中的第个位置;
(2)当N=2n(n≥8)时,x173位于P4中的第个位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线 ![]() =1(a,b>0)的两顶点为A1 , A2 , 虚轴两端点为B1 , B2 , 两焦点为F1 , F2 . 若以A1A2为直径的圆内切于菱形F1B1F2B2 , 切点分别为A,B,C,D.则: (Ⅰ)双曲线的离心率e=;
=1(a,b>0)的两顶点为A1 , A2 , 虚轴两端点为B1 , B2 , 两焦点为F1 , F2 . 若以A1A2为直径的圆内切于菱形F1B1F2B2 , 切点分别为A,B,C,D.则: (Ⅰ)双曲线的离心率e=;
(Ⅱ)菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值 ![]() = .
= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出直线![]() 的普通方程以及曲线
的普通方程以及曲线![]() 的极坐标方程;
的极坐标方程;
(2)若直线![]() 与曲线的
与曲线的![]() 两个交点分别为
两个交点分别为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com