
| A. | $(2k-\frac{1}{4},2k+\frac{1}{4}),k∈Z$ | B. | $(2k+\frac{1}{2},2k+\frac{5}{2}),k∈Z$ | ||
| C. | $(4k-\frac{1}{4},4k+\frac{1}{4}),k∈Z$ | D. | $(4k+\frac{1}{4},4k+\frac{15}{4}),k∈Z$ |
分析 根据条件判断函数的周期性和对称性,求出函数在一个周期内的解析式,利用转化法进行求解即可.
解答 解:∵f(x)是定义在R上的奇函数,且f(x-1)为偶函数,
∴f(-x-1)=f(x-1)=-f(x+1),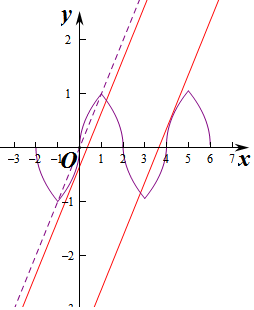
即f(x)=-f(x+2),
则f(x+4)=-f(x+2)=f(x),即函数f(x)的周期是4,
∵f(x-1)为偶函数,∴f(x-1)关于x=0对称,
则f(x)关于x=-1对称,同时也关于x=1对称,
若x∈[-1,0],则-x∈[0,1],
此时f(-x)=$\sqrt{-x}$=-f(x),则f(x)=-$\sqrt{-x}$,x∈[-1,0],
若x∈[-2,-1],x+2∈[0,1],
则f(x)=-f(x+2)=-$\sqrt{x+2}$,x∈[-2,-1],
若x∈[1,2],x-2∈[-1,0],
则f(x)=-f(x-2)=$\sqrt{-(x-2)}$=$\sqrt{2-x}$,x∈[1,2],
作出函数f(x)的图象如图:
由数g(x)=f(x)-x-b=0得f(x)=x+b,
由图象知当x∈[-1,0]时,由-$\sqrt{-x}$=x+b,平方得x2+(2b+1)x+b2=0,
由判别式△=(2b+1)2-4b2=0得4b+1=0,得b=-$\frac{1}{4}$,此时f(x)=x+b有两个交点,
当x∈[4,5],x-4∈[0,1],则f(x)=f(x-4)=$\sqrt{x-4}$,
由$\sqrt{x-4}$=x+b,平方得x2+(2b-1)x+4+b2=0,
由判别式△=(2b-1)2-16-4b2=0得4b=-15,得b=-$\frac{15}{4}$,此时f(x)=x+b有两个交点,
则要使此时f(x)=x+b有一个交点,则在[0,4]内,b满足-$\frac{15}{4}$<b<-$\frac{1}{4}$,
即实数b的取值集合是4n-$\frac{15}{4}$<b<4n-$\frac{1}{4}$,
即4(n-1)+$\frac{1}{4}$<b<4(n-1)+$\frac{15}{4}$,
令k=n-1,
则4k+$\frac{1}{4}$<b<4k+$\frac{15}{4}$,
故选:D
点评 本题主要考查函数零点的应用,根据函数的性质求出函数的周期性和对称性,利用数形结合是解决本题的关键.综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,4) | B. | [4,5) | C. | (-3,-2) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
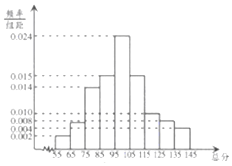 从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.
从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本,分别统计出这些试卷总分,由总分得到如下的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
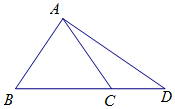 已知△ABC是等边三角形,D在BC的延长线上,且CD=2,${S_{△ABD}}=6\sqrt{3}$.
已知△ABC是等边三角形,D在BC的延长线上,且CD=2,${S_{△ABD}}=6\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果平面α⊥平面 γ,平面β⊥平面 γ,α∩β=l,那么l⊥γ | |
| B. | 如果平面α⊥平面 β,那么平面α内一定存在直线平行于平面β | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 如果平面α⊥平面 β,过α内任意一点作交线的垂线,那么此垂线必垂直于β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com