
【题目】(1)求![]() 的值;
的值;
(2)设m,n∈N*,n≥m,求证: ![]()
【答案】(1)0;(2)见解析
【解析】试题分析:(1)利用组合数公式计算即可;
(2)利用数学归纳法证明即可.
试题解析:(1)解 7C-4C=7×20-4×35=0.
(2)证明 对任意的m,n∈N*,n≥m,
①当n=m时,左边=(m+1)C=m+1,
右边=(m+1)C![]() =m+1,原等式成立.
=m+1,原等式成立.
②假设n=k(k≥m)时命题成立.
即(m+1)C+(m+2)C![]() +(m+3)C
+(m+3)C![]() +…+kC
+…+kC![]() +(k+1)C=(m+1)C
+(k+1)C=(m+1)C![]() ,
,
当n=k+1时,
左边=(m+1)C+(m+2)C![]() +(m+3)C
+(m+3)C![]() +…+kC
+…+kC![]() +(k+1)C+(k+2)C
+(k+1)C+(k+2)C![]()
=(m+1)C![]() +(k+2)C
+(k+2)C![]() ,
,
右边=(m+1)C![]() .
.
而(m+1)C![]() -(m+1)C
-(m+1)C![]()
=(m+1)![]()
=(m+1)×![]() [(k+3)-(k-m+1)]
[(k+3)-(k-m+1)]
=(k+2)![]() =(k+2)C
=(k+2)C![]() ,
,
∴(m+1)C![]() +(k+2)C
+(k+2)C![]() =(m+1)C
=(m+1)C![]() ,
,
∴左边=右边.
即m=k+1时命题也成立.
综合①②可得原命题对任意m,n∈N*,n≥m均成立.


科目:高中数学 来源: 题型:
【题目】为了反映各行业对仓储物流业务需求变化的情况,以及重要商品库存变化的动向,中国物流与采购联合会和中储发展股份有限公司通过联合调查,制定了中国仓储指数.由2016年1月至2017年7月的调查数据得出的中国仓储指数,绘制出如下的折线图.
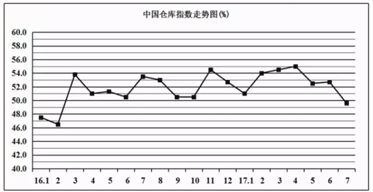
根据该折线图,下列结论正确的是( )
A. 2016年各月的合储指数最大值是在3月份
B. 2017年1月至7月的仓储指数的中位数为55
C. 2017年1月与4月的仓储指数的平均数为52
D. 2016年1月至4月的合储指数相对于2017年1月至4月,波动性更大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,圆C的参数方程为![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
![]() 1
1![]() 求圆C的普通方程和直线l的直角坐标方程;
求圆C的普通方程和直线l的直角坐标方程;
![]() 2
2![]() 设M是直线l上任意一点,过M做圆C切线,切点为A、B,求四边形AMBC面积的最小值.
设M是直线l上任意一点,过M做圆C切线,切点为A、B,求四边形AMBC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示,则下列判断正确的是( )
的部分图象如图所示,则下列判断正确的是( )

A. 函数的图象关于点![]() 对称
对称
B. 函数的图象关于直线![]() 对称
对称
C. 函数![]() 的最小正周期为
的最小正周期为![]()
D. 当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 围成的封闭图形面积为
围成的封闭图形面积为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥![]() 中,底边
中,底边![]() ,侧棱
,侧棱![]() ,
, ![]() 为侧棱
为侧棱![]() 上的点.
上的点.
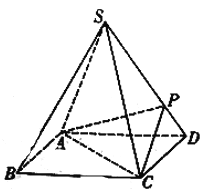
(1)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的余弦值的大小;
的余弦值的大小;
(2)若![]() ,侧棱
,侧棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,求
,若存在,求![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com