
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,且两焦点的距离为
,且两焦点的距离为![]() ,椭圆
,椭圆![]() 上一点与两焦点构成的三角形的周长为
上一点与两焦点构成的三角形的周长为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)设椭圆![]() 的标准方程为
的标准方程为![]() ,焦距为
,焦距为![]() ,根据题意可得
,根据题意可得![]() 、
、![]() ,可计算出
,可计算出![]() 的值,进而可得出椭圆
的值,进而可得出椭圆![]() 的标准方程;
的标准方程;
(2)由题意可知,直线![]() 不能与
不能与![]() 轴垂直,设直线
轴垂直,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,列出韦达定理,由
的方程联立,列出韦达定理,由![]() ,得出
,得出![]() ,利用平面向量数量积的坐标运算结合韦达定理求出实数
,利用平面向量数量积的坐标运算结合韦达定理求出实数![]() 的值,即可得出直线
的值,即可得出直线![]() 的方程.
的方程.
(1)设椭圆![]() 的标准方程为
的标准方程为![]() ,焦距为
,焦距为![]() ,
,
由题意可得 ,解得
,解得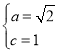 ,
,![]() ,
,
因此,椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)由题意可知,直线![]() 不能与
不能与![]() 轴垂直,
轴垂直,
设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线![]() 的方程与椭圆
的方程与椭圆![]() 的标准方程联立
的标准方程联立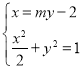 ,
,
消去![]() 并整理得
并整理得![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() .
.
由韦达定理得![]() ,
,![]() ,
,
![]() ,则
,则![]() ,且
,且![]() ,同理
,同理![]() ,
,
![]() ,解得
,解得![]() ,满足
,满足![]() .
.
综上所述,直线![]() 的方程为
的方程为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的空间几何体中,平面![]() 平面
平面![]() 与
与![]() 都是边长为2的等边三角形,
都是边长为2的等边三角形,![]() 与平面
与平面![]() 所成的角为60°,且点
所成的角为60°,且点![]() 在平面
在平面![]() 上的射影落在
上的射影落在![]() 的平分线上.
的平分线上.
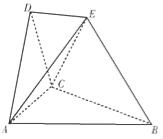
(1)求证:![]() 平面
平面![]() ;
;
(2)求四面体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆与圆![]() 相切,且与圆
相切,且与圆![]() 相内切,记圆心的轨迹为曲线.
相内切,记圆心的轨迹为曲线.
(Ⅰ)求曲线C的方程;
(Ⅱ)设Q为曲线C上的一个不在轴上的动点,O为坐标原点,过点![]() 作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
作OQ的平行线交曲线C于M,N两个不同的点, 求△QMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《流浪地球》是由刘慈欣的科幻小说改编的电影,在2019年春节档上影,该片上影标志着中国电影科幻元年的到来;为了振救地球,延续百代子孙生存的希望,无数的人前仆后继,奋不顾身的精神激荡人心,催人奋进.某网络调查机构调查了大量观众的评分,得到如下统计表:

(1)求观众评分的平均数?
(2)视频率为概率,若在评分大于等于8分的观众中随机地抽取1人,他的评分恰好是10分的概率是多少?
(3)视频率为概率,在评分大于等于8分的观众中随机地抽取4人,用![]() 表示评分为10分的人数,求
表示评分为10分的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】重庆一中将要举行校园歌手大赛,现有3男3女参加,需要安排他们的出场顺序.(结果用数字作答)
(1)如果3个女生都不相邻,那么有多少种不同的出场顺序?
(2)如果女生甲在女生乙的前面(可以不相邻),那么有多少种不同的出场顺序?
(3)如果3位男生都相邻,且女生甲不在第一个出场,那么有多少种不同的出场顺序?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是菱形,![]() ,BD=2.
,BD=2.
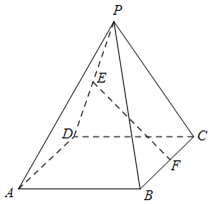
(1)若点E,F分别为线段PD,BC上的中点,求证:EF∥平面PAB;
(2)若平面PBD⊥平面ABCD,且PD⊥PB,PD=PB,求平面PAB与平面PBC所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com