
【题目】某校高一(1)(2)两个班联合开展“诗词大会进校园,国学经典润心田”古诗词竞赛主题班会活动,主持人从这两个班分别随机选出20名同学进行当场测试,他们的测试成绩按[40,50),[50,60),[60,70),[70,80),[80,90),[90,100)分组,分别用频率分布直方图与茎叶图统计如图(单位:分): 
高一(2)班20名学生成绩茎叶图:
4 | 5 |
5 | 2 |
6 | 4 5 6 8 |
7 | 0 5 5 8 8 8 8 9 |
8 | 0 0 5 5 |
9 | 4 5 |
(Ⅰ)分别计算两个班这20名同学的测试成绩在[80,90)的频率,并补全频率分布直方图;
(Ⅱ)分别从两个班随机选取1人,设这两人中成绩在[80,90)的人数为X,求X的分布列(频率当作概率使用).
(Ⅲ)运用所学统计知识分析比较两个班学生的古诗词水平.
【答案】解:(I)(1)班的同学成绩在[80,90)的频率为:1﹣(0.005+0.015+0.005+0.02+0.015)×10=0.4, 高一(2)班的同学成绩在[80,90)的频率为: ![]() =0.2.
=0.2.
补全频率分布直方图如下:
(II)(1)班成绩在[80,90)上的人数有20×0.4=8人,(2)班成绩在[80,90)上的人数有4人,
∴X的可能取值为0,1,2.
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() .
.
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
(III)由频率分布直方图看,(1)班的主要成绩集中在[70,100)上,
从茎叶图看,(2)班的主要成绩集中在(60,80)上,
故(1)班的古诗词水平好于(2)班的古诗词水平
【解析】(I)根据面积之和等于1计算(1)班成绩在[80,90)的频率;直角根据公式计算(2)班成绩在[80,90)的频率;(II)利用组合数公式计算概率;(III)根据数据的集中程度得出结论.
【考点精析】本题主要考查了频率分布直方图和离散型随机变量及其分布列的相关知识点,需要掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把函数f(x)=cos2( ![]() x﹣
x﹣ ![]() )的图象向左平移
)的图象向左平移 ![]() 个单位后得到的函数为g(x),则以下结论中正确的是( )
个单位后得到的函数为g(x),则以下结论中正确的是( )
A.g( ![]() )>g(
)>g( ![]() )>0
)>0
B.g( ![]() )
) ![]() ??
??
C.g( ![]() )>g(
)>g( ![]() )>0
)>0
D.g( ![]() )=g(
)=g( ![]() )>0
)>0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中xOy,直线C1的参数方程为 ![]() (t是参数).在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρ=sinθ﹣cosθ(θ是参数).
(t是参数).在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρ=sinθ﹣cosθ(θ是参数).
(Ⅰ)将曲线C2的极坐标方程化为直角坐标方程,并判断曲线C2所表示的曲线;
(Ⅱ)若M为曲线C2上的一个动点,求点M到直线C1的距离的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
![]() ( m 为常数).
( m 为常数).
(Ⅰ)若曲线 y f x 在点 0, f 0 处的切线斜率为 1 ,求实数 m 的值.
(Ⅱ)求函数 f x 的极值.
(Ⅲ)证明:当 x 0 时,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
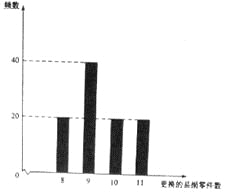
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记![]() 表示2台机器三年内共需更换的易损零件数,
表示2台机器三年内共需更换的易损零件数,![]() 表示购买2台机器的同时购买的易损零件数.
表示购买2台机器的同时购买的易损零件数.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)若要求![]() ,确定
,确定![]() 的最小值;
的最小值;
(Ⅲ)以购买易损零件所需费用的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com