
 如图,某房子屋檐A点离地面15米.房子上另一点B离地面9米,而且A,B两点在同一铅垂线上,在离地面7米的C处看此房子,问水平距离离此房子多远时A,B的视角(∠ACB)最大?
如图,某房子屋檐A点离地面15米.房子上另一点B离地面9米,而且A,B两点在同一铅垂线上,在离地面7米的C处看此房子,问水平距离离此房子多远时A,B的视角(∠ACB)最大? 分析 设C处离此房子x米时看A,B的视角(即∠ACB)最大,过C点作CD⊥AB于D点由图可知 AD=8,BD=2,CD=x,进而表示出tan∠BCD与tan∠ACD,利用两角和与差的正切函数公式表示出tan∠ACB,利用基本不等式求出视角最大时x的值即可.
解答 解:设C处离此房子x米时看A,B的视角(即∠ACB)最大.
过C点作CD⊥AB于D点由图可知 AD=8,BD=2,CD=x …(3分)
在Rt△ACD中,tan∠ACD=$\frac{8}{x}$
在Rt△BCD中,tan∠BCD=$\frac{2}{x}$
∴tan∠ACB=tan(∠ACD-∠BCD)=$\frac{\frac{8}{x}-\frac{2}{x}}{1+\frac{8}{x}•\frac{2}{x}}$=$\frac{6}{x+\frac{16}{x}}$≤$\frac{3}{4}$ …(9分)
当且仅当x=$\frac{16}{x}$,即x=4时取等号 …(10分)
∴水平距离离房子4米时,视角最大. …(12分)
点评 此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.


科目:高中数学 来源: 题型:选择题

| A. | -45 | B. | 13 | C. | -13 | D. | -37 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,3) | B. | (-3,-4) | C. | (-$\frac{3}{5}$,$\frac{4}{5}$) | D. | (-$\frac{3}{5}$,-$\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
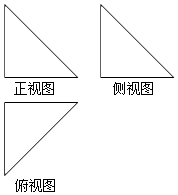 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,若直角三角形的直角边为2,那么这个几何体的表面积为( )
如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,若直角三角形的直角边为2,那么这个几何体的表面积为( )| A. | $\frac{4}{3}$ | B. | 6+2$\sqrt{2}$ | C. | 6+2$\sqrt{3}$ | D. | 12+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错导致结论错 | B. | 小前提错导致结论错 | ||
| C. | 推理形式错导致结论错 | D. | 大前提和小前提错导致结论错 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| A. | (4,5.5) | B. | (4,5) | C. | (5,5) | D. | (6,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com