
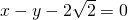 相切.
相切.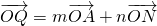 ,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;
,(其中m+n=1,m,n≠0,m为常数),试求动点Q的轨迹方程C2;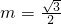 时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.
时,得到曲线C,问是否存在与l1垂直的一条直线l与曲线C交于B、D两点,且∠BOD为钝角,请说明理由.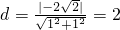 …(2分)
…(2分)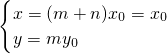 …(5分)
…(5分)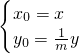 ,将
,将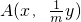 代入x2+y2=4,得
代入x2+y2=4,得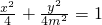 …(7分)
…(7分)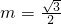 时,曲线C方程为
时,曲线C方程为 ,假设存在直线l与直线l1:
,假设存在直线l与直线l1: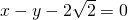 垂直,
垂直, 交点B(x1,y1),D(x2,y2)
交点B(x1,y1),D(x2,y2)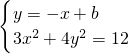 ,得7x2-8bx+4b2-12=0…(9分)
,得7x2-8bx+4b2-12=0…(9分)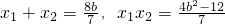 …(10分)
…(10分)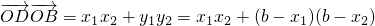 =
=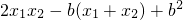
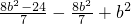 =
=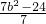 …(12分)
…(12分)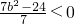 且b≠0,
且b≠0,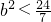 且b≠0,满足b2<7
且b≠0,满足b2<7 且b≠0,
且b≠0,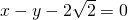 相切,利用点到直线的距离,求出圆的半径,从而可求圆C1的方程;
相切,利用点到直线的距离,求出圆的半径,从而可求圆C1的方程;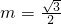 时,曲线C方程为
时,曲线C方程为 ,假设直线l的方程,与椭圆
,假设直线l的方程,与椭圆 联立,利用韦达定理及向量条件,利用数量积小于0,即可得到结论.
联立,利用韦达定理及向量条件,利用数量积小于0,即可得到结论.

科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 是
是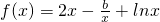 的一个极值点.
的一个极值点.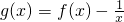 ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?查看答案和解析>>
科目:高中数学 来源: 题型:单选题
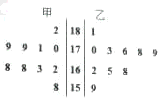 随机抽取某花场甲,乙两种计划在植树节期间移种的树苗各10株,测量它们的高度(单位:cm),获得高度数据的茎叶图如图,则下列关于甲、乙两种各10株树苗高度的结论正确的是
随机抽取某花场甲,乙两种计划在植树节期间移种的树苗各10株,测量它们的高度(单位:cm),获得高度数据的茎叶图如图,则下列关于甲、乙两种各10株树苗高度的结论正确的是查看答案和解析>>
科目:高中数学 来源: 题型:填空题
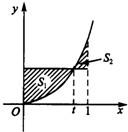 已知函数f(x)=ex-1,直线l1:x=1,l2:y=et-1(t为常数,且0≤t≤1),直线l1,l2与函数f(x)的图象围成的封闭图形,以及直线l2,y轴与函数f(x)的图象围成的封闭图形如图中阴影所示.当t变化时阴影部分的面积的最小值为________.
已知函数f(x)=ex-1,直线l1:x=1,l2:y=et-1(t为常数,且0≤t≤1),直线l1,l2与函数f(x)的图象围成的封闭图形,以及直线l2,y轴与函数f(x)的图象围成的封闭图形如图中阴影所示.当t变化时阴影部分的面积的最小值为________.查看答案和解析>>
科目:高中数学 来源: 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com