
分析 构造函数f(x)=ax2-2x+1,利用根的存在性定理,列出不等式组$\left\{\begin{array}{l}{f(0)•f(1)<0}\\{f(1)•f(2)<0}\end{array}\right.$,求出解集即可.
解答 解:设f(x)=ax2-2x+1,
∵关于x的方程ax2-2x+1=0的一个根在(0,1)上,另一个根在(1,2)上,
∴$\left\{\begin{array}{l}{f(0)•f(1)<0}\\{f(1)•f(2)<0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a-1<0}\\{(a-1)(4a-3)<0}\end{array}\right.$,
解得$\frac{3}{4}$<a<1;
∴a的取值范围是($\frac{3}{4}$,1).
点评 本题考查了方程的根与函数零点的应用问题,解题时应结合零点的存在定理,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广西陆川县中学高二理9月月考数学试卷(解析版) 题型:解答题
在 中,
中, 分别为角
分别为角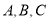 的对边,若
的对边,若 .
.
(1)求角 的大小;
的大小;
(2)已知 ,求
,求 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com