分析:(1)设F
n+2+λF
n+1=q(F
n+1+λF
n)(q≠0)则F
n+2=(q-λ)F
n+1+qλF
n,又因为F
n+2=F
n+1+F
n,所以
,由此能够求出所有λ的值,并求出数列{F
n}的通项公式.
(2)由F
n>0,知F
n+2=F
n+1+F
n>F
n+1,{F
n}为递增数列.所以F
n+2=F
n+1+F
n>F
n+F
n,即F
n+2>2F
n.由此入手能够证明
++…+<.
解答:解:(1)设F
n+2+λF
n+1=q(F
n+1+λF
n)(q≠0),
则F
n+2=(q-λ)F
n+1+qλF
n又因为F
n+2=F
n+1+F
n
∴
,
解得
或------(3分);
∴
数列{Fn+1+Fn}和{Fn+1+Fn}都是等比数列∴
两式相减得,
Fn=[()n-()n]----(8分);
(2)证:显然F
n>0,
∴F
n+2=F
n+1+F
n>F
n+1,
∴{F
n}为递增数列.
∴F
n+2=F
n+1+F
n>F
n+F
n,
即F
n+2>2F
n----(12分);
∴F
7>2F
5=2×5,F
9>2F
7>2
2F
5=2
2×5,…,
F
2007>2F
2005>2
2F
2003>…>2
1001F
5=2
1001×5
∴F
8>2F
6=2×8,F
10>2F
8>2
2F
6=2
2×8,…,
F
2006>2F
2004>2
2F
2002>…>2
1000F
6=2
1000×8---(16分);
+
(++…+)+(+=
++++×+×
<+++++∴
++…+<--(20分);
点评:本题考查数列与不等式的综合应用能力,综合性强,难度是高考的重点,计算繁琐,容易出错.解题时要认真审题,注意培养计算能力,注意合理地进行等价转化.



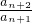 -
- =e(e为常数),则称数列{an}为比等差数列,e称为比公差.现给出下列命题:
=e(e为常数),则称数列{an}为比等差数列,e称为比公差.现给出下列命题: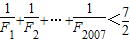 .
. -
- =e(e为常数),则称数列{an}为比等差数列,e称为比公差.现给出下列命题:
=e(e为常数),则称数列{an}为比等差数列,e称为比公差.现给出下列命题: