
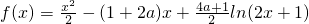 .
. -3x+
-3x+ ln(2x+1),x>-
ln(2x+1),x>- ,
, =
= =
= ,…(1分)
,…(1分) 或x=2…(2分)
或x=2…(2分)| x | (- , , ) ) |  | ( ,2) ,2) | 2 | (2,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大 | ↙ | 极小 | ↗ |
 ,
, …(5分)
…(5分) =
= =
=
 或x=2a…(6分)
或x=2a…(6分) ,即a>
,即a> 时,
时,| x | (- , , ) ) |  | ( ,2a) ,2a) | 2a | (2a,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | ↙ | ↗ |
 ,
, )和(2a,+∞),减区间为(
)和(2a,+∞),减区间为( ,2a)…(8分)
,2a)…(8分) ,即a=
,即a= 时,f'(x)=
时,f'(x)= ≥0在(
≥0在( ,+∞)上恒成立,
,+∞)上恒成立, ,+∞)…(10分)
,+∞)…(10分) <2a<
<2a< ,即-
,即- <a<
<a< 时,
时,| x | (- ,2a) ,2a) | 2a | (2a, ) ) |  | ( ,+∞) ,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | ↙ | ↗ |
 ,2a)和(
,2a)和( ,+∞),减区间为(2a,
,+∞),减区间为(2a, )…(12分)
)…(12分) ,即a≤-
,即a≤- 时,
时,| x | (- , , ) ) |  | ( ,+∞) ,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↙ | ↗ |
 ,+∞),减区间为(-
,+∞),减区间为(- ,
, )…(14分)
)…(14分) 时,f(x)的增区间为(
时,f(x)的增区间为( ,+∞),减区间为(-
,+∞),减区间为(- ,
, )-
)- <a<
<a< 时,f(x)的增区间为(-
时,f(x)的增区间为(- ,2a)和(
,2a)和( ,+∞),减区间为(2a,
,+∞),减区间为(2a, )a=
)a= 时,f(x)的增区间为(
时,f(x)的增区间为( ,+∞)a>
,+∞)a> 时,f(x)的增区间为(-
时,f(x)的增区间为(- ,
, )和(2a,+∞),减区间为(
)和(2a,+∞),减区间为( ,2a)
,2a) -3x+
-3x+ ln(2x+1),x>-
ln(2x+1),x>- ,可求得f′(x)=
,可求得f′(x)= ,通过将x、f(x)、f′(x)的变化情况列表可求得函数f(x)极大值和极小值;
,通过将x、f(x)、f′(x)的变化情况列表可求得函数f(x)极大值和极小值; ,通过比较2a与-
,通过比较2a与- ,2a与
,2a与 的大小,分类讨论,利用函数单调性与极值之间的关系即可求得函数f(x)的单调区间.
的大小,分类讨论,利用函数单调性与极值之间的关系即可求得函数f(x)的单调区间.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源:2011-2012学年山西省高三年级第四次四校联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知函数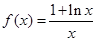 .
.
(1)设a>0,若函数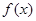 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(2)如果当x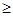 1时,不等式
1时,不等式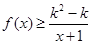 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省营口市开发区一中高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
 .
. ,都有f(x)<-2,求实数a的取值范围.
,都有f(x)<-2,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省营口市开发区一中高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
 .
. ,都有f(x)<-2,求实数a的取值范围.
,都有f(x)<-2,求实数a的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省六校高三第四次联考数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com