
…,用反证法证明a3=2.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试理科数学(北京卷解析版) 题型:解答题
已知{an}是由非负整数组成的无穷数列,该数列前n项的最大值记为An,第n项之后各项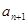 ,
, …的最小值记为Bn,dn=An-Bn.
…的最小值记为Bn,dn=An-Bn.
(I)若{an}为2,1,4,3,2,1,4,3…,是一个周期为4的数列(即对任意n∈N*,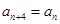 ),写出d1,d2,d3,d4的值;
),写出d1,d2,d3,d4的值;
(II)设d为非负整数,证明:dn=-d(n=1,2,3…)的充分必要条件为{an}为公差为d的等差数列;
(III)证明:若a1=2,dn=1(n=1,2,3…),则{an}的项只能是1或2,且有无穷多项为1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com