
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() ,
,![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)当![]() ,
,![]() 时,求证方程
时,求证方程![]() 在区间
在区间![]() 上有唯一实数根;
上有唯一实数根;
(3)当![]() 时,设
时,设![]() 是
是![]() 函数两个不同的极值点,证明:
函数两个不同的极值点,证明:![]() .
.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】
(1)构造新函数y=![]() ,求导判断单调性,得出最小值e.(2)变量分离a=-
,求导判断单调性,得出最小值e.(2)变量分离a=-![]() =h(x),根据函数的单调性求出函数h(x)的最小值,利用a的范围证明在区间(0,2)上有唯一实数根;(3)求出
=h(x),根据函数的单调性求出函数h(x)的最小值,利用a的范围证明在区间(0,2)上有唯一实数根;(3)求出![]() ,问题转化为证
,问题转化为证![]() ,令x1﹣x2=t,得到t<0,根据函数的单调性证明即可.
,令x1﹣x2=t,得到t<0,根据函数的单调性证明即可.
(1)当![]() =0,
=0,![]() 时,
时,![]() =
=![]() ,求导y’=
,求导y’=![]() =0的根x=1
=0的根x=1
所以y在(-![]() ),(0,1)递减,在(1,+
),(0,1)递减,在(1,+![]() )递增,
)递增,
所以y![]() =e
=e
(2)![]() +
+![]() =0,所以a=-
=0,所以a=-![]() =h(x)
=h(x)
H’(x)=-![]() =0的根x=2
=0的根x=2
则h(x)在(0,2)上单调递增,在(2,+∞)上单调递减,
所以h(2)是y=h(x)的极大值即最大值,即![]()
所以函数f(x)在区间(0,2)上有唯一实数根;
(3)![]() =
= ![]() -
-![]()
F’(x)![]() -2ax-a=0的两根是
-2ax-a=0的两根是![]() ,
,![]()
∵x1,x2是函数F(x)的两个不同极值点(不妨设x1<x2),
∴a>0(若a≤0时,f'(x)>0,即F(x)是R上的增函数,与已知矛盾),
且F'(x1)=0,F'(x2)=0.∴![]() ,
,![]() …
…
两式相减得: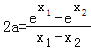 ,…
,…
于是要证明![]() ,即证明
,即证明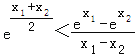 ,两边同除以
,两边同除以![]() ,
,
即证 ,即证
,即证![]() ,即证
,即证![]() ,
,
令x1﹣x2=t,t<0.即证不等式![]() ,当t<0时恒成立.
,当t<0时恒成立.
设![]() ,∴
,∴![]() =
=![]()
设![]() ,∴
,∴![]() ,
,
当t<0,h'(t)<0,h(t)单调递减,
所以h(t)>h(0)=0,即![]() ,
,
∴φ'(t)<0,∴φ(t)在t<0时是减函数.
∴φ(t)在t=0处取得极小值φ(0)=0.
∴φ(t)>0,得证.
∴![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某中学举行一次“环保知识竞赛”,全校学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为![]() 分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
分)作为样本进行统计,请根据下面尚未完成并有局部污损的样本的频率分布表和频率分布直方图(如图所示)解决下列问题:
(Ⅰ)写出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(Ⅱ)在选取的样本中,从竞赛成绩是![]() 分以上(含
分以上(含![]() 分)的同学中随机抽取
分)的同学中随机抽取![]() 名同学到广场参加环保知识的志愿宣传活动,求所抽取的
名同学到广场参加环保知识的志愿宣传活动,求所抽取的![]() 名同学来自同一组的概率.
名同学来自同一组的概率.
(Ⅲ)在(Ⅱ)的条件下,设![]() 表示所抽取的
表示所抽取的![]() 名同学中来自第
名同学中来自第![]() 组的人数,求
组的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
组别 | 分组 | 频数 | 频率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合计 |
|
|

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中随机抽取了200人进行抽样分析,得到下表(单位:人):
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所有抽取的30岁以上的网民中利用分层抽样抽取5人,
![]() 求这5人中经常使用、偶尔或不用共享单车的人数;
求这5人中经常使用、偶尔或不用共享单车的人数;
![]() 从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
从这5人中,在随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式: 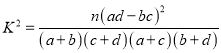 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC![]() 中,侧面
中,侧面![]() 是矩形,∠BAC=90°,
是矩形,∠BAC=90°,![]() ⊥BC,
⊥BC,![]() =AC=2AB=4,且
=AC=2AB=4,且![]() ⊥
⊥![]() .
.

(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)设D是![]() 的中点,判断并证明在线段
的中点,判断并证明在线段![]() 上是否存在点E,使得DE∥平面
上是否存在点E,使得DE∥平面![]() .若存在,求二面角E
.若存在,求二面角E![]() B的余弦值.
B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
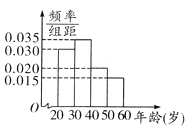
【题目】某工厂有120名工人,其年龄都在20~ 60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分成四组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试。已知各年龄段两项培训结业考试成绩优秀的人数如下表所示。假设两项培训是相互独立的,结业考试也互不影响。
年龄分组 | A项培训成绩 优秀人数 | B项培训成绩 优秀人数 |
[20,30) | 27 | 16 |
[30,40) | 28 | 18 |
[40,50) | 16 | 9 |
[50,60] | 6 | 4 |
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求四个年龄段应分别抽取的人数;
(2)根据频率分布直方图,估计全厂工人的平均年龄;
(3)随机从年龄段[20,30)和[40,50)中各抽取1人,设这两人中A、B两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
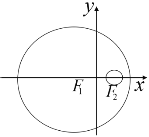
【题目】如图,已知圆![]() 的方程为
的方程为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,若动圆
,若动圆![]() 与圆
与圆![]() 内切,与圆
内切,与圆![]() 外切.
外切.
(Ⅰ)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过直线![]() 上的点
上的点![]() 作圆
作圆![]() 的两条切线,设切点分别是
的两条切线,设切点分别是![]() ,
,![]() ,若直线
,若直线![]() 与轨迹
与轨迹![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,试求函数y=![]() (x>0)的最小值;
(x>0)的最小值;
(2)对于任意的x∈[0,2],不等式f(x)≤a成立,试求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com