
| 2 |
| 2 |
| ||
| 3 |
| c |
| a |
| ||
| 3 |
| 2 |
| 3 |
| a2-c2 |
| x2 |
| 3 |
|
| 3(1-t2) |
| 3(1-t2) |
| ||
| 2 |
| ||
| 2 |
| 3(1-t2)-x2 |
| 3(1-t2) |
| 3(1-t2) |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
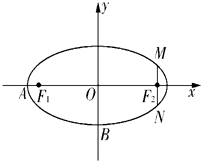 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:| y2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| PA |
| AB |
查看答案和解析>>
科目:高中数学 来源:广东省揭阳市2007年高中毕业班第一次高考模拟考试题(理科) 题型:044
如图,在直角坐标系xOy中,已知椭圆![]() 的离心率e=
的离心率e=![]() ,左右两个焦分别为F1、F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=1.
,左右两个焦分别为F1、F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点,且|MN|=1.
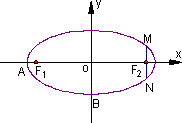
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C的左顶点为A,下顶点为B,动点P满足![]() ,(
,(![]() )试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省湛江二中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
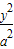 +
+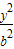 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=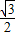 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的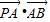 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
查看答案和解析>>
科目:高中数学 来源:2010年内蒙古赤峰市高三统考数学试卷(文科)(解析版) 题型:解答题
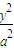 +
+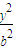 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=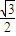 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的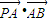 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.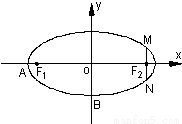
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com