
(本小题满分12分)已知某商品的价格上涨x%,销售的数量就减少mx%,其中m为正的常数。
(1)当m=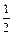 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
(2)如果适当地涨价,能使销售总金额增加,求m的取值范围
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本题满分14分,第(1)小题7分,第(2)小题7分)
某地发生特大地震和海啸,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质。已 知每投放质量为
知每投放质量为 的药剂后,经过
的药剂后,经过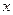 天该药剂在水中释放的浓度
天该药剂在水中释放的浓度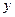 (毫克/升) 满足
(毫克/升) 满足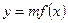 ,其中
,其中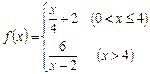 ,当药剂在水中释放的浓度不低于
,当药剂在水中释放的浓度不低于 (毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于
(毫克/升)时称为有效净化;当药剂在水中释放的浓度不低于 (毫克/升) 且不高于10(毫克/升)时称为最佳净化。
(毫克/升) 且不高于10(毫克/升)时称为最佳净化。
(1)如果投放的药剂质量为 ,试问自来水达到有效净化一共可持续几天?
,试问自来水达到有效净化一共可持续几天?
(2)如果投放的药剂质量为 ,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量
,为了使在7天之内(从投放药剂算起包括7天)的自来水达到最佳净化,试确定应该投放的药剂质量 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分15分)某经销商用一辆J型卡车将某种水果从果园运送(满载)到相距400km的水果批发市场.据测算,J型卡车满载行驶时,每100km所消耗的燃油量u(单位:
资、车损等其他费用平均每小时300元.已知燃油价格为每升(L)7.5元.
(1)设运送这车水果的费用为y(元)(不计返程费用),将y表示成速度v的函数关系式;
(2)卡车该以怎样的速度行驶,才能使运送这车水果的费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题11分)如图,矩形ABCD中,AB=6,BC=2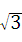 ,点O是AB的中点,点P在AB的延长线
,点O是AB的中点,点P在AB的延长线 上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点
上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点 出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积 为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;
为S,求出S与t之间的函数关系式和相应的自变量t的取值范围;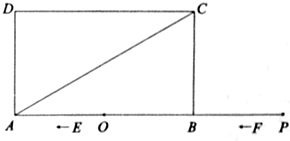
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 的图象与x轴有两个不同的公共点,且
的图象与x轴有两个不同的公共点,且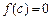 ,当
,当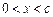 时,恒有
时,恒有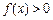 .
.
(1)当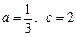 时,求不等式
时,求不等式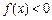 的解集;
的解集;
(2)若以二次函数的图象与坐标轴的三个交点为顶点的三角形的面积为8,且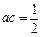 ,求a的值;
,求a的值;
(3)若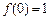 ,且
,且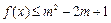 对所有
对所有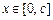 恒成立,求正实数m的最小值.
恒成立,求正实数m的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某地方政府为地方电子工业发展,决定对某一进口电子产品征收附加税。已知这种电子产品国内市场零售价为每件250元,每年可销售40万件,若政府征收附加税率为t元时,则每年减少 y万件。
y万件。
(1)收入表示为征收附加税率的函数;
(2)在 该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
该项经营中每年征收附加税金不低于600万元,那么附加税率应控制在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分)若定义在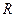 上的函数
上的函数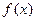 同时满足下列三个条件:
同时满足下列三个条件:
①对任意实数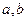 均有
均有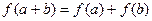 成立;
成立;
②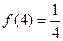 ;
;
③当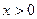 时,都有
时,都有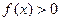 成立。
成立。
(1)求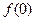 ,
,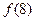 的值;
的值;
(2)求证: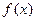 为
为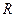 上的增函数
上的增函数
(3)求解关于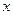 的不等式
的不等式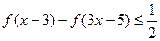 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com