
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,AP段围墙造价为每平方米150元,AQ段围墙造价为每平方米100元.若围围墙用了30000元,问如何围可使竹篱笆用料最省?
【答案】
(1)解:∵AP+AQ=200,
∴S= ![]() ≤
≤ ![]() =2500
=2500 ![]() .
.
当且仅当x=y=100时取“=”.
∴当x=y=100时,可使得三角形地块APQ的面积最大.
(2)解:设AP=x,AQ=y,则1x150+1.5y100=30000,
化为:x+y=200≥2 ![]() ,可得xy≤10000.
,可得xy≤10000.
∴PQ2=x2+y2﹣2xycos120°=x2+y2+xy=(x+y)2﹣xy=40000﹣xy≥30000.
当且仅当x=y=100时取“=”.
即PQ≥100 ![]() .
.
∴当且仅当x=y=100时,可使PQ取得最小值,即使用竹篱笆用料最省.
【解析】(1)先求出三角形地块APQ的面积,再利用基本不等式可得三角形地块APQ的面积最大;(2)先利用余弦定理可得PQ2,再利用基本不等式可得PQ的最小值.
【考点精析】掌握基本不等式是解答本题的根本,需要知道基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,且a3=-6,a6=0.
(1)求{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求{bn}的前n项和公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年5月12日,国家统计局公布了《2013年农民工监测调查报告》,报告显示:我国农
民工收入持续快速增长.某地区农民工人均月收入增长率如图1,并将人均月收入绘制成如
图2的不完整的条形统计图.

图1 图2
根据以上统计图来判断以下说法错误的是
A. 2013年农民工人均月收入的增长率是![]()
B. 2011年农民工人均月收入是![]() 元
元
C. 小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了”
D. 2009年到2013年这五年中2013年农民工人均月收入最高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点O在![]() 内,且满足
内,且满足![]() ,设
,设![]() 为
为![]() 的面积,
的面积, ![]() 为
为![]() 的面积,则
的面积,则![]() =________.
=________.
【答案】![]()
【解析】由![]() ,可得:
,可得: ![]()
延长OA,OB,OC,使OD=2OA,OE=4OB,OF=3OC,
如图所示:

∵2![]() +3
+3![]() +4
+4![]() =
=![]() ,
,
∴![]() ,
,
即O是△DEF的重心,
故△DOE,△EOF,△DOF的面积相等,
不妨令它们的面积均为1,
则△AOB的面积为![]() ,△BOC的面积为
,△BOC的面积为![]() ,△AOC的面积为
,△AOC的面积为![]() ,
,
故三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() :
: ![]() :
: ![]() =3:2:4,
=3:2:4,
![]() .
.
故答案为: ![]() .
.
点睛:本题考查的知识点是三角形面积公式,三角形重心的性质,平面向量在几何中的应用,注意重要结论:点O在![]() 内,且满足
内,且满足![]() ,
, ![]() 则三角形△AOB,△BOC,△AOC的面积之比依次为:
则三角形△AOB,△BOC,△AOC的面积之比依次为: ![]() .
.
【题型】填空题
【结束】
16
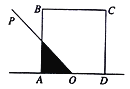
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记![]() 为
为![]() OP所经过的在正方形ABCD内的区域(阴影部分)的面积
OP所经过的在正方形ABCD内的区域(阴影部分)的面积![]() ,那么对于函数
,那么对于函数![]() 有以下三个结论:
有以下三个结论:
①![]() ;
;
②任意![]() ,都有
,都有![]() ;
;
③任意![]() 且
且![]() ,都有
,都有![]() .
.
其中正确结论的序号是__________. (把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,过点P(2,1)的直线l的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,已知直线l与曲线C交于A、B两点.
(t为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,已知直线l与曲线C交于A、B两点.
(1)求曲线C的直角坐标方程;
(2)求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记![]() 为
为![]() OP所经过的在正方形ABCD内的区域(阴影部分)的面积
OP所经过的在正方形ABCD内的区域(阴影部分)的面积![]() ,那么对于函数
,那么对于函数![]() 有以下三个结论:
有以下三个结论:
①![]() ;
;
②任意![]() ,都有
,都有![]() ;
;
③任意![]() 且
且![]() ,都有
,都有![]() .
.
其中正确结论的序号是__________. (把所有正确结论的序号都填上).

【答案】①②
【解析】试题分析:①:如图,当![]() 时,
时, ![]() 与
与![]() 相交于点
相交于点![]() ,∵
,∵![]() ,则
,则![]() ,
,
∴![]() ,∴①正确;②:由于对称性,
,∴①正确;②:由于对称性, ![]() 恰好是正方形的面积,
恰好是正方形的面积,
∴![]() ,∴②正确;③:显然
,∴②正确;③:显然![]() 是增函数,∴
是增函数,∴![]() ,∴③错误.
,∴③错误.

考点:函数性质的运用.
【题型】填空题
【结束】
17
【题目】化简
(1)![]()
(2)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的通项公式为
的通项公式为![]() (
(![]() ,
, ![]() ),数列
),数列![]() 定义如下:对于正整数
定义如下:对于正整数![]() ,
, ![]() 是使得不等式
是使得不等式![]() 成立的所有
成立的所有![]() 中的最小值.
中的最小值.
(1)若![]() ,
, ![]() ,求
,求![]() ;
;
(2)若![]() ,
, ![]() ,求数列
,求数列![]() 的前
的前![]() 项和公式;
项和公式;
(3)是否存在![]() 和
和![]() ,使得
,使得![]()
![]() ?如果存在,求
?如果存在,求![]() 和
和![]() 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com