与直线3x+y-10=0平行的曲线y=x3-3x2+1的切线方程为 .
【答案】
分析:设出切点,求出函数在切点处的导数,因为所求切线与直线3x+y-10=0平行,所以所求导数值等于-3,由此求出切点的横坐标,代入曲线方程求出切点的纵坐标,由直线方程的点斜式写出直线方程,最后化为一般式.
解答:解:设与直线3x+y-10=0平行且与曲线y=x
3-3x
2+1相切的切线与曲线的切点为(

),
由y=x
3-3x
2+1,得y
′=3x
2-6x,则

=
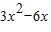
.
所以
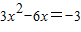
,即
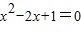
,所以x
=1.
则
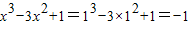
.
所以切点为(1,-1).
所以切线方程为y-(-1)=-3×(x-1).即为3x+y-2=0.
故答案为3x+y-2=0.
点评:本题考查了利用导数研究函数在某点的切线方程问题,考查了导数的几何意义,函数在某点处的导数,就是函数在该点的切线的斜率.此题是中档题.

 ),
), =
=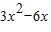 .
.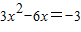 ,即
,即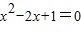 ,所以x=1.
,所以x=1.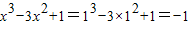 .
.
