
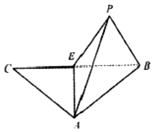
 等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.
等腰△ABC,E为底边BC的中点,沿AE折叠,如图,将C折到点P的位置,使二面角P-AE-C的大小为120°,设点P在面ABE上的射影为H.分析 (I)证明:∠CEP为二面角C-AE-P的平面角,则点P在面ABE上的射影H在EB上,即可证明点H为EB的中点;
(II)过H作HM⊥AB于M,连PM,过H作HN⊥PM于N,连BN,则有三垂线定理得AB⊥面PHM.即面PHM⊥面PAB,HN⊥面PAB.故HB在面PAB上的射影为NB,∠HBN为直线BE与面ABP所成的角,即可求直线BE与平面ABP所成角的正弦值.
解答  (I)证明:依题意,AE⊥BC,则AE⊥EB,AE⊥EP,EB∩EP=E.
(I)证明:依题意,AE⊥BC,则AE⊥EB,AE⊥EP,EB∩EP=E.
∴AE⊥面EPB.
故∠CEP为二面角C-AE-P的平面角,则点P在面ABE上的射影H在EB上.
由∠CEP=120°得∠PEB=60°.…(3分)
∴EH=$\frac{1}{2}$EP=$\frac{1}{2}$EB.
∴H为EB的中点.…(6分)
(II)解:过H作HM⊥AB于M,连PM,过H作HN⊥PM于N,连BN,
则有三垂线定理得AB⊥面PHM.即面PHM⊥面PAB,
∴HN⊥面PAB.故HB在面PAB上的射影为NB.
∴∠HBN为直线BE与面ABP所成的角.…(9分)
依题意,BE=$\frac{1}{2}$BC=2,BH=$\frac{1}{2}$BE=1.
在△HMB中,HM=$\frac{\sqrt{2}}{2}$,
在△EPB中,PH=$\sqrt{3}$,
∴在Rt△PHM中,HN=$\frac{\sqrt{21}}{7}$.
∴sin∠HBN=$\frac{\sqrt{21}}{7}$,tan∠HBN=$\frac{\sqrt{3}}{2}$.…(12分)
点评 本题考查线面垂直,考查线面角,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | (1,2] | C. | [-2,1) | D. | [-3,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[\frac{{3\sqrt{2}}}{2},\sqrt{5}]$ | B. | $[\frac{{3\sqrt{2}}}{2},5]$ | C. | $[\frac{9}{2},5]$ | D. | $[\sqrt{5},\frac{9}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{14}{68}$ | B. | $\frac{21}{68}$ | C. | $\frac{68}{14}$ | D. | $\frac{68}{21}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com