
【题目】设函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 、
、![]() .
.
(Ⅱ)设![]() ,求
,求![]() 的最大值.
的最大值.
(Ⅲ)证明函数![]() 的图像与直线
的图像与直线![]() 没有公共点.
没有公共点.
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,设
为常数,设![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(2)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,若
,若![]() ,对于任意的两个正实数
,对于任意的两个正实数![]() ,证明:
,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足: ![]() ,
, 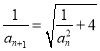 ,
, ![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,试确定
,试确定![]() 的值,使得数列
的值,使得数列![]() 为等差数列;
为等差数列;
(3)将数列![]() 中的部分项按原来顺序构成新数列
中的部分项按原来顺序构成新数列![]() ,且
,且![]() ,求证:存在无数个满足条件的无穷等比数列
,求证:存在无数个满足条件的无穷等比数列![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
, ![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
B. 把![]() 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
C. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
D. 把曲线![]() 向右平移
向右平移![]() 个单位长度,再把得到的曲线上各点横坐标缩短到原来的
个单位长度,再把得到的曲线上各点横坐标缩短到原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问某地100名高中学生在选择座位时是否挑同桌,得到如下![]() 列联表:
列联表:
男生 | 女生 | 合计 | |
挑同桌 | 30 | 40 | 70 |
不挑同桌 | 20 | 10 | 30 |
总计 | 50 | 50 | 100 |
![]() Ⅰ
Ⅰ![]() 从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
从这50名男生中按是否挑同桌采取分层抽样的方法抽取一个容量为5的样本,现从这5人中随机选取3人做深度采访,求这3名学生中至少有2名要挑同桌的概率;
![]() Ⅱ
Ⅱ![]() 根据以上
根据以上![]() 列联表,是否有
列联表,是否有![]() 以上的把握认为“性别与在选择座位时是否挑同桌”有关?
以上的把握认为“性别与在选择座位时是否挑同桌”有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() 参考公式:
参考公式: ![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com