
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,![]()
【解析】
(1)将点![]() 代入椭圆方程得到
代入椭圆方程得到![]() ,结合基本不等式,求得
,结合基本不等式,求得![]() 取得最小值时
取得最小值时![]() ,进而证得椭圆的离心率为
,进而证得椭圆的离心率为![]() .
.
(2)当直线![]() 的斜率不存在时,根据椭圆的对称性,求得
的斜率不存在时,根据椭圆的对称性,求得![]() 到直线
到直线![]() 的距离.当直线
的距离.当直线![]() 的斜率存在时,联立直线
的斜率存在时,联立直线![]() 的方程和椭圆方程,写出韦达定理,利用
的方程和椭圆方程,写出韦达定理,利用![]() ,则
,则![]() 列方程,求得
列方程,求得![]() 的关系式,进而求得
的关系式,进而求得![]() 到直线
到直线![]() 的距离.根据上述分析判断出所求的圆存在,进而求得定圆的方程.
的距离.根据上述分析判断出所求的圆存在,进而求得定圆的方程.
(1)证明:∵椭圆![]() 经过点
经过点![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
此时椭圆![]() 的离心率
的离心率![]() .
.
(2)解:∵椭圆![]() 的焦距为2,∴
的焦距为2,∴![]() ,又
,又![]() ,∴
,∴![]() ,
,![]() .
.
当直线![]() 的斜率不存在时,由对称性,设
的斜率不存在时,由对称性,设![]() ,
,![]() .
.
∵![]() ,
,![]() 在椭圆
在椭圆![]() 上,∴
上,∴![]() ,∴
,∴![]() ,∴
,∴![]() 到直线
到直线![]() 的距离
的距离![]() .
.
当直线![]() 的斜率存在时,设
的斜率存在时,设![]() 的方程为
的方程为![]() .
.
由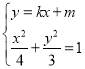 ,得
,得![]() ,
,
![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 到直线
到直线![]() 的距离
的距离![]() .
.
综上,![]() 到直线
到直线![]() 的距离为定值,且定值为
的距离为定值,且定值为![]() ,故存在定圆
,故存在定圆![]() :
:![]() ,使得圆
,使得圆![]() 与直线
与直线![]() 总相切.
总相切.


科目:高中数学 来源: 题型:
【题目】甲、乙两人各进行![]() 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率
,乙每次击中目标的概率![]() ,
,
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅱ)求甲恰好比乙多击中目标![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,
,![]() ,
,![]() ,
,![]() 是其左右顶点,点
是其左右顶点,点![]() 是椭圆
是椭圆![]() 上任一点,且
上任一点,且![]() 的周长为6,若
的周长为6,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过点![]() 且斜率不为0的直线交椭圆
且斜率不为0的直线交椭圆![]() 于
于![]() ,
,![]() 两个不同点,证明:直线
两个不同点,证明:直线![]() 与
与![]() 的交点在一条定直线上.
的交点在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司新开发一电子产品,该电子产品的一个系统G有3个电子元件组成,各个电子元件能否正常工作的概率均为![]() ,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
(1)求系统不需要维修的概率;
(2)该电子产品共由3个系统G组成,设E为电子产品需要维修的系统所需的费用,求![]() 的分布列与期望;
的分布列与期望;
(3)为提高G系统正常工作概率,在系统内增加两个功能完全一样的其他品牌的电子元件,每个新元件正常工作的概率均为![]() ,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:
,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:![]() 满足什么条件时,可以提高整个G系统的正常工作概率?
满足什么条件时,可以提高整个G系统的正常工作概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为认真贯彻落实党中央国务院决策部署,坚持“房子是用来住的,不是用来炒的”定位,坚持调控政策的连续性和稳定性,进一步稳定某省市商品住房市场,该市人民政府办公厅出台了相关文件来控制房价,并取得了一定效果,下表是2019年2月至6月以来该市某城区的房价均值数据:
| 2 | 3 | 4 | 5 | 6 |
| 9.80 | 9.70 |
| 9.30 | 9.20 |
已知:![]() .
.![]()
(1)若变量![]() 、
、![]() 具有线性相关关系,求房价均价
具有线性相关关系,求房价均价![]() (千元/平方米)关于月份
(千元/平方米)关于月份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测该市某城区7月份的房价.
(参考公式:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式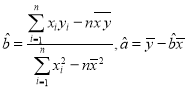 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
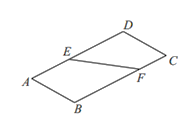
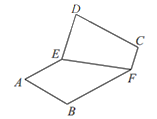
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次![]() 普查,为此需要抽验1000人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.方案①:将每个人的血分别化验,这时需要验1000次.方案②:按
普查,为此需要抽验1000人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.方案①:将每个人的血分别化验,这时需要验1000次.方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血只需检验一次(这时认为每个人的血化验
个人的血只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这样,该组
个人的血样再分别进行一次化验,这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.假设此次普查中每个人的血样化验呈阳性的概率为
次.假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人的每个人的血化验次数为
个人的每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() ,试比较方案②中,分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
,试比较方案②中,分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com