
分析 由三角形函数公式化简可得$\frac{sin2α-2co{s}^{2}α}{sin(α-\frac{π}{4})}$=$\frac{2cosα(sinα-cosα)}{\frac{\sqrt{2}}{2}(sinα-cosα)}$,约分可得.
解答 解:化简可得$\frac{sin2α-2co{s}^{2}α}{sin(α-\frac{π}{4})}$=$\frac{2sinαcosα-2co{s}^{2}α}{\frac{\sqrt{2}}{2}(sinα-cosα)}$
=$\frac{2cosα(sinα-cosα)}{\frac{\sqrt{2}}{2}(sinα-cosα)}$=2$\sqrt{2}$cosα,
故答案为:2$\sqrt{2}$cosα.
点评 本题考查三角函数的化简求值,涉及二倍角公式和和差角的三角函数公式,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
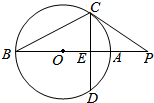 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com