
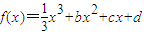 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).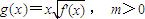 ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值; ×27-32+3+d=0得:d=-3
×27-32+3+d=0得:d=-3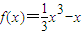 2+x-3
2+x-3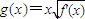 =x|x-1|
=x|x-1| )2-
)2- ,函数为增函数
,函数为增函数 )2+
)2+ ,最大为g(
,最大为g( )=
)=
 得:m≥
得:m≥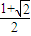 时,m(m-1)≥
时,m(m-1)≥
 时,g(x)的最大值为m-m2;
时,g(x)的最大值为m-m2;
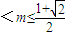 时,g(x)的最大值为
时,g(x)的最大值为 ;
;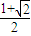 时,g(x)最大值为m2-m
时,g(x)最大值为m2-m

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:2012-2013学年辽宁省本溪一中高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).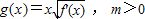 ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值;查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省本溪一中高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
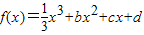 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).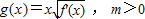 ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值;查看答案和解析>>
科目:高中数学 来源:2013年高考数学压轴大题训练:函数的最值问题(解析版) 题型:解答题
 ,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x).
,设曲线y=f(x)在与x轴交点处的切线为y=4x-12,f′(x)为f(x)的导函数,且满足f′(2-x)=f′(x). ,求函数g(x)在[0,m]上的最大值;
,求函数g(x)在[0,m]上的最大值;查看答案和解析>>
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷三文科数学 题型:解答题
(本小题满分14分)已知函数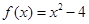 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n Î N *),x1=4.
(Ⅰ)用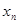 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg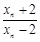 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较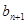 与
与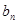 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com