
【题目】如图,正方体ABCD﹣A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.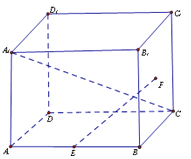
【答案】解:(1)取BC中点H,连结FH,EH,设正方体棱长为2.
∵F为BCC1B1中心,E为AB中点.
∴FH⊥平面ABCD,FH=1,EH=![]() .
.
∴∠FEH为直线EF与平面ABCD所成角,且FH⊥EH.
∴tan∠FEH=![]() =
=![]() =
=![]() .
.
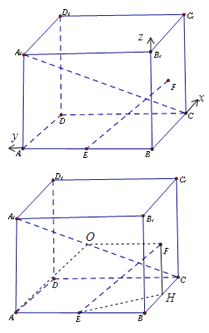
(2)取A1C中点O,连接OF,OA,则OF∥AE,且OF=AE.
∴四边形AEFO为平行四边形.∴AO∥EF.
∴∠AOA1为异面直线A1C与EF所成角.
∵A1A=2,AO=A1O=![]() .
.
∴△AOA1中,由余弦定理得cos∠A1OA=![]() .
.
【解析】(1)取BC中点H,连结FH,EH,证明∠FEH为直线EF与平面ABCD所成角,即可得出结论;
(2)取A1C中点O,连接OF,OA,则∠AOA1为异面直线A1C与EF所成角,由余弦定理,可得结论;
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】样本a1 , a2 , a3 , …,a10的平均数为 ![]() ,样本b1 , b2 , b3 , …,b10的平均数为
,样本b1 , b2 , b3 , …,b10的平均数为 ![]() ,那么样本a1 , b1 , a2 , b2 , …,a10 , b10的平均数为( )
,那么样本a1 , b1 , a2 , b2 , …,a10 , b10的平均数为( )
A.![]() +
+ ![]()
![]()
B.![]() (
( ![]() +
+ ![]() )
)![]()
C.2( ![]() +
+ ![]() )
)
D.![]() (
( ![]() +
+ ![]() )
)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的参数方程;
的参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,试求
上动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知焦点在x轴上的椭圆 ![]() =1(b>0)有一个内含圆x2+y2=
=1(b>0)有一个内含圆x2+y2= ![]() ,该圆的垂直于x轴的切线交椭圆于点M,N,且
,该圆的垂直于x轴的切线交椭圆于点M,N,且 ![]() ⊥
⊥ ![]() (O为原点).
(O为原点). 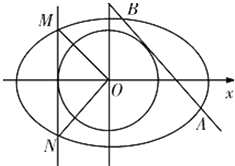
(1)求b的值;
(2)设内含圆的任意切线l交椭圆于点A、B.求证: ![]() ,并求|
,并求| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,△ABC是底面,PA⊥PB,PA⊥PC,PB⊥PC,且这四个顶点都在半径为2的球面上,PA=2PB,则这个三棱锥的三个侧棱长的和的最大值为( )
A.16
B.![]()
C.![]()
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,x∈[2,5].
,x∈[2,5].
(1)判断函数f(x)的单调性,并用定义证明你的结论;
(2)求不等式f(m+1)<f(2m﹣1)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣alnx(a∈R).
(Ⅰ)当a=2时,求曲线f(x)在x=1处的切线方程;
(Ⅱ)设函数h(x)=f(x)+![]() , 求函数h(x)的单调区间;
, 求函数h(x)的单调区间;
(Ⅲ)若g(x)=﹣![]() , 在[1,e](e=2.71828…)上存在一点x0 , 使得f(x0)≤g(x0)成立,求a的取值范围.
, 在[1,e](e=2.71828…)上存在一点x0 , 使得f(x0)≤g(x0)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017陕西渭南二模】若函数![]() 的图象上存在两个点
的图象上存在两个点![]() 关于原点对称,则对称点
关于原点对称,则对称点![]() 为
为![]() 的“孪生点对”,点对
的“孪生点对”,点对![]() 与
与![]() 可看作同一个“孪生点对”,若函数
可看作同一个“孪生点对”,若函数![]() 恰好有两个“孪生点对”,则实数
恰好有两个“孪生点对”,则实数![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com