
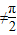 +kπ,k∈z|};
+kπ,k∈z|};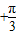 )的图象的一条对称轴为x=-
)的图象的一条对称轴为x=-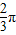 ;
; ,k∈z|};
,k∈z|}; +kπ,k∈z|}不正确;
+kπ,k∈z|}不正确; )的图象的一条对称轴为x=-
)的图象的一条对称轴为x=-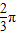 ;因为cos[2×
;因为cos[2×
 ]=cos(-π)=-1,函数取得最值,所以③是正确的.
]=cos(-π)=-1,函数取得最值,所以③是正确的. 实数根的个数是2.所以判断不正确.
实数根的个数是2.所以判断不正确.

科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| 2 |
| 3 |
| 1 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
在下列结论中:
①函数![]()
![]() 为奇函数;
为奇函数;
②函数![]() 的最小正周期是
的最小正周期是![]() ;
;
③函数![]() 的图象的一条对称轴为
的图象的一条对称轴为![]() ;
;
④函数![]() 在
在![]() 上单调减区间是
上单调减区间是![]() .
.
其中正确结论的序号为 (把所有正确结论的序号都填上)。
查看答案和解析>>
科目:高中数学 来源:山东省济南外国语学校10-11学年高一下学期期末考试数学 题型:填空题
在下列结论中:
①函数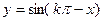 (k∈Z)为奇函数;
(k∈Z)为奇函数;
②函数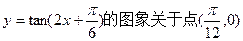 对称;
对称;
③函数 ;
;
④若
其中正确结论的序号为 (把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源:2011年黑龙江省七校高一上学期期末考试数学试卷 题型:填空题
.在下列结论中:
①函数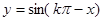
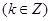 为奇函数;
为奇函数;
② ;
;
③函数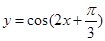 的图象的一条对称轴为
的图象的一条对称轴为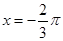 ;
;
④方程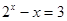 的实根个数为1个。 其中正确结论的序号为
的实根个数为1个。 其中正确结论的序号为
(把所有正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com