
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 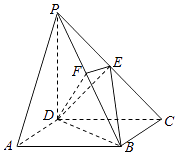
(1)求证:PA∥平面BDE;
(2)求证:PB⊥平面DEF.
【答案】
(1)证明:连结AC,设AC交BD于O,连结EO,
∵底面ABCD中矩形,∴点O是AC的中点,
又∵点E是PC的中点,∴PA∥EO,
∵EO平面BDE,PA平面BDE,
∴PA∥平面EO
(2)证明:PD⊥底面ABCD,BC底面ABCD,
∴PD⊥BC,
∵底面ABCD中矩形,∴CD⊥BC,
∵PD∩CD=D,∴BC⊥平面PDC,
∵DE平面PDC,∴BC⊥DE,
∵PD=DC,E是PC的中点,∴DE⊥PC,
∵PC∩BC=C,∴DE⊥PB,
又∵EF⊥PB,DE∩EF=E,DE平面DEF,EF平面DEF,
∴PB⊥平面DEF.
【解析】(1)连结AC,设AC交BD于O,连结EO,则PA∥EO,由此能证明PA∥平面EO.(2)由已知得PD⊥BC,CD⊥BC,从而BC⊥平面PDC,进而BC⊥DE,再由DE⊥PC,DE⊥PB,由此能证明PB⊥平面DEF.
【考点精析】关于本题考查的直线与平面平行的判定和直线与平面垂直的判定,需要了解平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
【题目】抽样调查某大型机器设备使用年限x和该年支出维修费用y(万元),得到数据如表
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
部分数据分析如下 ![]() =25,
=25, ![]() yi=112.3,
yi=112.3, ![]() =90
=90
参考公式:线性回归直线方程为 ![]() ,
, 
(1)求线性回归方程;
(2)由(1)中结论预测第10年所支出的维修费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+m21﹣x .
(1)若函数f(x)为奇函数,求实数m的值;
(2)若函数f(x)在区间(1,+∞)上是单调递增函数,求实数m的取值范围;
(3)是否存在实数a,使得函数f(x)的图象关于点A(a,0)对称,若存在,求实数a的值,若不存在,请说明理由.
注:点M(x1 , y1),N(x2 , y2)的中点坐标为( ![]() ,
, ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+(b﹣8)x﹣a﹣ab的两个零点分别是﹣3和2.
(Ⅰ)求f(x);
(Ⅱ)当函数f(x)的定义域是[0,1]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班20名同学某次数学测试的成绩可绘制成如图茎叶图.由于其中部分数据缺失,故打算根据茎叶图中的数据估计全班同学的平均成绩.


(1)完成频率分布直方图;
(2)根据(1)中的频率分布直方图估计全班同学的平均成绩![]() (同一组中的数据用改组区间的中点值作代表);
(同一组中的数据用改组区间的中点值作代表);
(3)根据茎叶图计算出的全班的平均成绩为![]() ,并假设
,并假设![]() ,且
,且![]() 取得每一个可能值的机会相等,在(2)的条件下,求概率
取得每一个可能值的机会相等,在(2)的条件下,求概率![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数g(x)=log2 ![]() (x>0),关于方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,则实数m的取值范围为( )
(x>0),关于方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,则实数m的取值范围为( )
A.(﹣∞,4﹣2 ![]() )∪(4
)∪(4 ![]() ,+∞)
,+∞)
B.(4﹣2 ![]() ,4
,4 ![]() )
)
C.(﹣ ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com