
【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.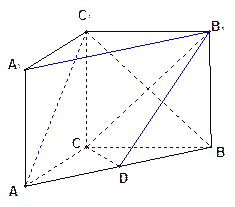
【答案】![]()
【解析】
试题分析:(1)由勾股定理计算得AC⊥BC,再由直棱柱性质得C1C⊥AC,最后根据线面垂直判定定理得AC⊥平面BCC1B1,即得AC⊥BC1.(2)设CB1与C1B的交点为E,由三角形中位线性质得DE∥AC1,再根据线面平行判定定理得结论(3)因为DE∥AC1,所以∠CED为AC1与B1C所成的角.再根据解三角形得所成角的余弦值.
试题解析:(1)证明:在直三棱柱ABC-A1B1C1中,底面三边长AC=3,BC=4,AB=5,∴AC⊥BC.
又∵C1C⊥AC.∴AC⊥平面BCC1B1.
∵BC1平面BCC1B,∴AC⊥BC1.
(2)证明:设CB1与C1B的交点为E,连接DE,又四边形BCC1B1为正方形.
∵D是AB的中点,E是BC1的中点,∴DE∥AC1.
∵DE平面CDB1,AC1平面CDB1,
∴AC1∥平面CDB1.
(3)∵DE∥AC1,
∴∠CED为AC1与B1C所成的角.在△CED中,ED=![]() AC1=
AC1=![]() ,
,
CD=![]() AB=
AB=![]() ,CE=
,CE=![]() CB1=2
CB1=2![]() ,∴cos∠CED=
,∴cos∠CED=![]() =
=![]() .
.
∴异面直线AC1与B1C所成角的余弦值为![]() .
.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=e2x+ln(x+a).
(1)当a=1时,①求f(x)在(0,1)处的切线方程;②当x≥0时,求证:f(x)≥(x+1)2+x.
(2)若存在x0∈[0,+∞),使得 ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理” 的原则,规定参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有![]() 三家社区医院,并且他们的选择是等可能的、相互独立的.
三家社区医院,并且他们的选择是等可能的、相互独立的.
(1)求甲、乙两人都选择![]() 社区医院的概率;
社区医院的概率;
(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设在4名参加保险人员中选择![]() 社区医院的人数为
社区医院的人数为![]() ,求
,求![]() 的分布列和数学期望及方差.
的分布列和数学期望及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司进行仓储机器人升级换代期间,第一年有机器人![]() 台,平均每台机器人创收利润
台,平均每台机器人创收利润![]() 万元.预测以后每年平均每台机器人创收利润都比上一年增加
万元.预测以后每年平均每台机器人创收利润都比上一年增加![]() 万元,但该物流公司在用机器人数量每年都比上一年减少
万元,但该物流公司在用机器人数量每年都比上一年减少![]() .
.
(1)设第![]() 年平均每台机器人创收利润为
年平均每台机器人创收利润为![]() 万元,在用机器人数量为
万元,在用机器人数量为![]() 台,求
台,求![]() ,
,![]() 的表达式;
的表达式;
(2)依上述预测,第几年该物流公司在用机器人创收的利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=
,PB= ![]()
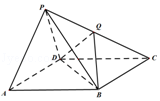
(Ⅰ)求证:平面PAD⊥平面ABCD;
(Ⅱ)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y+1=0,l2:-2x+y+2=0,它们相交于点A.
(1)判断直线l1和l2是否垂直?请给出理由.
(2)求过点A且与直线l3:3x+y+4=0平行的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=pe﹣x+x+1(p∈R). (Ⅰ)当实数p=e时,求曲线y=f(x)在点x=1处的切线方程;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)当p=1时,若直线y=mx+1与曲线y=f(x)没有公共点,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com