考点:二面角的平面角及求法,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由已知直三棱柱ABC-A1B1C1中,∠ABC=90,易得AB⊥平面BB1C1C,从而可得AB⊥DB1;由2AB=2BC=CC1=2,D是棱CC1的中点可证B1D2+BD2=BB12,即可证BD⊥B1D,从而可证;
(2)由(1)知BD⊥B1D,AD⊥B1D,则∠ADB就是平面AB1D与侧面BB1C1C的成角的平面角,Rt△ABD中求解∠ADB即可.
解答:
(1)证明:在Rt△B
1C
1D中,∠B
1C
1D=90°,B
1C
1=1,C
1D=
C1C=1
∴B
1D=
,同理BD=
在△B
1DB中,∵B
1D
2+BD
2=B
1B
2,∴∠B
1DB=90°
即B
1D⊥BD,
又∵在直三棱柱ABC-A
1B
1C
1中,∠ABC=90°
∴AB⊥平面BB
1C
1C,而B
1D?平面BB
1C
1C,∴B
1D⊥AB,
∵AB∩BD=B,∴B
1D⊥平面ABD;
(2)解:由(1)知BD⊥B
1D,AD⊥B
1D,平面AB
1D∩平面BB
1C
1C=B
1D
∴∠ADB就是平面AB
1D与侧面BB
1C
1C的成角的平面角
在Rt△ABD中,∠ABD=90°,AB=1,BD=
∴cos∠ADB=
.
点评:本小题主要考查空间中线面关系,二面角及其平面角等基础知识,考查空间想象能力、逻辑推理能力和运算求解能力.

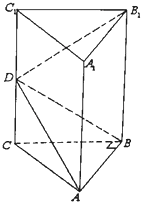 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案