
【题目】已知函数![]() ,其图像与
,其图像与![]() 轴切于非原点的一点,且该函数的极小值是
轴切于非原点的一点,且该函数的极小值是![]() ,那么切点坐标为______.
,那么切点坐标为______.
【答案】(-3,0)
【解析】
设切点(a,0)(a≠0),f(x)=x(x2+px+q).由题意得:方程x2+px+q=0有两个相等实根a,故可得f(x)=x(x﹣a)2=x3﹣2ax2+a2x,再利用y极小值=﹣4,可求a=﹣3,从而得到切点.
解:设切点(a,0)(a≠0),
f(x)=x(x2+px+q),
由题意得:方程x2+px+q=0有两个相等实根a,
故可得f(x)=x(x﹣a)2=x3﹣2ax2+a2x
f′(x)=3x2﹣4ax+a2=(x﹣a)(3x﹣a),
令f′(x)=0,则x=a或![]() ,
,
∵f(a)=0≠﹣4,
∴f(![]() )=﹣4,
)=﹣4,
于是![]() (
(![]() a)2=﹣4,
a)2=﹣4,
∴a=﹣3,
即有切点为(﹣3,0),
故答案为:(﹣3,0).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定义域;
的解析式及定义域;
(2)若函数![]() 在区间
在区间![]() 上为单调函数,求实数k的范围;
上为单调函数,求实数k的范围;
(3)若关于x的方程![]() 有解,求实数m的取值范围.
有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+bx+c(a,b,c∈R),若x=﹣1为函数y=f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是( )
A. 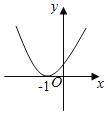 B.
B. 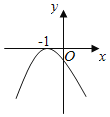
C. 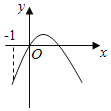 D.
D. 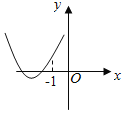
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把定义域为![]() 且同时满足以下两个条件的函数
且同时满足以下两个条件的函数![]() 称为“
称为“![]() 函数”:(1)对任意的
函数”:(1)对任意的![]() ,总有
,总有![]() ;(2)若
;(2)若![]() ,
,![]() ,则有
,则有![]() 成立,下列判断正确的是( )
成立,下列判断正确的是( )
A.若![]() 为“
为“![]() 函数”,则
函数”,则![]()
B.若![]() 为“
为“![]() 函数”,则
函数”,则![]() 在
在![]() 上为增函数
上为增函数
C.函数![]() 在
在![]() 上是“
上是“![]() 函数”
函数”
D.函数![]() 在
在![]() 上是“
上是“![]() 函数”
函数”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过函数性质的学习,我们知道:“函数![]() 的图象关于
的图象关于![]() 轴成轴对称图形”的充要条件是“
轴成轴对称图形”的充要条件是“![]() 为偶函数”.
为偶函数”.
(1)若![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ,求
,求![]() 的解析式,并求不等式
的解析式,并求不等式![]() 的解集;
的解集;
(2)某数学学习小组针对上述结论进行探究,得到一个真命题:“函数![]() 的图象关于直线
的图象关于直线![]() 成轴对称图形”的充要条件是“
成轴对称图形”的充要条件是“![]() 为偶函数”.若函数
为偶函数”.若函数![]() 的图象关于直线
的图象关于直线![]() 对称,且当
对称,且当![]() 时,
时,![]() .
.
(i)求![]() 的解析式;
的解析式;
(ii)求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
(1)求该椭圆的标准方程;
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)过原点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,求
两点,求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着雾霾的日益严重,中国部分省份已经实施了“煤改气”的计划来改善空气质量指数.2017年支撑我国天然气市场消费增长的主要资源是国产常规气和进口天然气,资源每年的增量不足以支撑天然气市场连续![]() 亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在
亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在![]() 亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续
亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(AQI),数据统计如下:
天监测空气质量指数(AQI),数据统计如下:
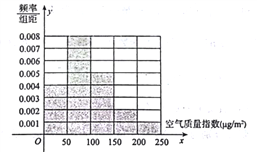
(1)根据上图完成下列表格
空气质量指数( |
|
|
|
|
|
天数 |
(2)计算这![]() 天中,该市空气质量指数的平均数;
天中,该市空气质量指数的平均数;
(3)若按照分层抽样的方法,从空气质量指数在![]() 以及
以及![]() 的等级中抽取
的等级中抽取![]() 天进行调研,再从这
天进行调研,再从这![]() 天中任取
天中任取![]() 天进行空气颗粒物分析,求恰有
天进行空气颗粒物分析,求恰有![]() 天空气质量指数在
天空气质量指数在![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com