【题目】在如图所示的五面体
中，四边形
为菱形，且
为
中点.
(Ⅰ)求证： 
平面
；
(Ⅱ)若平面
平面
，求
到平面
的距离.
【答案】(Ⅰ）见解析；(Ⅱ) 
.
【解析】试题分析：（1）取
中点
，连接
，根据线面平行的判定推出导出
平面
，由线面平行的性质得到
，进而得到四边形
为平行四边形.所以
，得到线面平行；（2）由（1）得
平面
，所以
到平面
的距离等于
到平面
的距离，由
，可求得点面距.
解析：(Ⅰ）取
中点
，连接
，
因为
分别为
中点，所以
，且
因为四边形
为菱形，所以
, 
平面
， 
平面
所以
平面
．
因为平面
平面
， 
平面
所以
又
，所以
.
所以四边形
为平行四边形.所以
.
又
平面
且
平面
，所以
平面
(Ⅱ)由（1）得
平面
，所以
到平面
的距离等于
到平面
的距离．
取
的中点
，连接
，
因为四边形
为菱形，且
， 
，
所以
， 
，因为平面
平面
，
平面
平面
，所以
平面
， 
，
因为
，所以
，
所以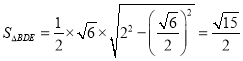
，
设
到平面
的距离为
，又因为
，
所以由
，得
，解得
.
即
到平面
的距离为
．
名师点拨卷系列答案科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）若
， 
都是从0，1，2，3，4五个数中任取的一个数，求上述函数有零点的概率；
（2）若
， 
都是从区间
上任取的一个数，求
成立的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，几何体是圆柱的一部分，它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的，G是
的中点.
(1)设P是
上的一点，且AP⊥BE，求∠CBP的大小；
(2)当AB＝3，AD＝2时，求二面角E－AG－C的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，
是
的直径，PA垂直于所在的平面，C是圆周上不同于A，B的一动点.
（1）证明：
是直角三角形；
（2）若
，且当直线
与平面
所成角的正切值为
时，求直线与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行调查，通过抽样，获得某年100为居民每人的月均用水量（单位：吨），将数据按照
分成9组，制成了如图所示的频率分布直方图.
（1）求直方图的
的值；
（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由.
（3）估计居民月用水量的中位数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如下图所示:
得出下面四个结论:
①甲同学的逻辑排名比乙同学的逻辑排名更靠前
②乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
③甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前
④甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前
则所有正确结论的序号是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
