
【题目】已知定义在R上的偶函数f(x)在(﹣∞,0]上单调递增,且f(﹣1)=﹣1.若f(x﹣1)+1≥0,则x的取值范围是_____;设函数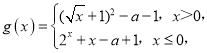 若方程f(g(x))+1=0有且只有两个不同的实数解,则实数a的取值范围为_____.
若方程f(g(x))+1=0有且只有两个不同的实数解,则实数a的取值范围为_____.
【答案】[0,2] (﹣∞,﹣1]∪(3,+∞).
【解析】
根据f(x)的奇偶性和单调性列不等式求出x的范围,根据g(x)的单调性和最值,分情况讨论最值和±1的关系,从而确定a的范围.
由f(x)是偶函数,且f(x)在![]() 上单调递增,
上单调递增,
所以f(x)在(0,+∞)上单调递减,且f(1)=f(﹣1)=﹣1,
由f(x﹣1)+1≥0可得:f(x﹣1)≥f(1),
所以﹣1≤x﹣1≤1,即0≤x≤2.
由f(g(x))+1=0可得g(x)=1或g(x)=﹣1.
由函数解析式可知g(x)在(﹣∞,0]和(0,+∞)上均为增函数,
故当x∈(﹣∞,0]时,g(x)≤2﹣a,当x∈(0,+∞)时,g(x)>﹣a,
(1)若1>2﹣a>﹣1>﹣a,则g(x)=1有1解,g(x)=﹣1有2解,不符合题意;
(2)若2﹣a>1>﹣a>﹣1,此时g(x)=1有2解,g(x)=﹣1有1解,不符合题意;
(3)若﹣a≥1,则g(x)=1有1解,g(x)=﹣1有1解,符合题意;
(4)若2﹣a<﹣1,则g(x)=1有1解,g(x)=﹣1有1解,符合题意;
(5)若2﹣a=1,则g(x)=1有2解,g(x)=﹣1有1解,不符合题意;
(6)若2﹣a=﹣1,则g(x)=﹣1有2解,g(x)=1有1解,不符合题意;
综上,﹣a≥1或2﹣a<﹣1,解得a≤﹣1或a>3.
故答案为:[0,2],(﹣∞,﹣1]∪(3,+∞).


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,P为直线
中,P为直线![]() :
:![]() 上的动点,动点Q满足
上的动点,动点Q满足![]() ,且原点O在以
,且原点O在以![]() 为直径的圆上.记动点Q的轨迹为曲线C
为直径的圆上.记动点Q的轨迹为曲线C
(1)求曲线C的方程:
(2)过点![]() 的直线
的直线![]() 与曲线C交于A,B两点,点D(异于A,B)在C上,直线
与曲线C交于A,B两点,点D(异于A,B)在C上,直线![]() ,
,![]() 分别与x轴交于点M,N,且
分别与x轴交于点M,N,且![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国的西气东输工程把西部的资源优势变为经济优势,实现了气能源需求与供给的东西部衔接,工程建设也加快了西部及沿线地区的经济发展输气管道工程建设中,某段管道铺设要经过一处峡谷,峡谷内恰好有一处直角拐角,水平横向移动输气管经过此拐角,从宽为![]() 米峡谷拐入宽为
米峡谷拐入宽为![]() 米的峡谷.如图所示,位于峡谷悬崖壁上两点
米的峡谷.如图所示,位于峡谷悬崖壁上两点![]() 、
、![]() 的连线恰好经过拐角内侧顶点
的连线恰好经过拐角内侧顶点![]() (点
(点![]() 、
、![]() 、
、![]() 在同一水平面内),设
在同一水平面内),设![]() 与较宽侧峡谷悬崖壁所成角为
与较宽侧峡谷悬崖壁所成角为![]() ,则
,则![]() 的长为________(用
的长为________(用![]() 表示)米.要使输气管顺利通过拐角,其长度不能低于________米.
表示)米.要使输气管顺利通过拐角,其长度不能低于________米.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆C:![]() 的左、右焦点,椭圆C过点M
的左、右焦点,椭圆C过点M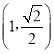 ,且MF2⊥F1F2.
,且MF2⊥F1F2.
(1)求椭圆C的方程;
(2)经过点P(2,0)的直线交椭圆C于A,B两点,若存在点Q(m,0),使得|QA|=|QB|.
①求实数m的取值范围:
②若线段F1A的垂直平分线过点Q,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x-a|+|2x-1|(a∈R).
(1)当a=-1时,求f(x)≤2的解集;
(2)若f(x)≤|2x+1|的解集包含集合![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=n2+pn,且a4,a7,a12成等比数列.
(1)求数列{an}的通项公式;
(2)若bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电讯企业为了了解某地区居民对电讯服务质量评价情况,随机调查100 名用户,根据这100名用户对该电讯企业的评分,绘制频率分布直方图,如图所示,其中样本数据分组为![]() ,
,![]() ,……
,……![]() .
.
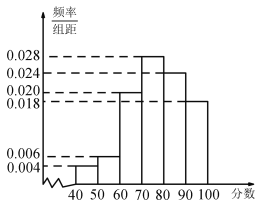
(1)估计该地区用户对该电讯企业评分不低于70分的概率,并估计对该电讯企业评分的中位数;
(2)现从评分在![]() 的调查用户中随机抽取2人,求2人评分都在
的调查用户中随机抽取2人,求2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com