【题目】已知椭圆和双曲线有共同焦点
，
是它们的一个交点，且
，记椭圆和双曲线的离心率分别为
，则
的最大值为（ ）
A. 3B. 2C. 
D. 
【答案】D
【解析】
设椭圆长半轴长为a1，双曲线的半实轴长a2，焦距2c．根据椭圆及双曲线的定义可以用a1，a2表示出|PF1|，|PF2|，在△F1PF2中根据余弦定理可得到
，利用基本不等式可得结论．
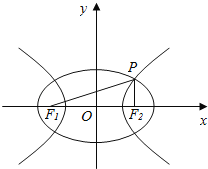
如图，设椭圆的长半轴长为a1，双曲线的半实轴长为a2，则根据椭圆及双曲线的定义：|PF1|+|PF2|＝2a1，|PF1|﹣|PF2|＝2a2，∴|PF1|＝a1+a2，|PF2|＝a1﹣a2，
设|F1F2|＝2c，∠F1PF2＝
，则：在△PF1F2中，由余弦定理得，
4c2＝（a1+a2）2+（a1﹣a2）2﹣2（a1+a2）（a1﹣a2）cos
∴化简得：a12+3a22＝4c2，该式可变成：，
∴≥2
∴
，
故选：D．
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目：高中数学 来源： 题型：
【题目】某中学为了解高一学生的视力健康状况，在高一年级体检活动中采用统一的标准对数视力表，按照《中国学生体质健康监测工作手册》的方法对1039名学生进行了视力检测，判断标准为：双眼裸眼视力
为视力正常， 
为视力低下，其中
为轻度， 
为中度， 
为重度.统计检测结果后得到如图所示的柱状图.
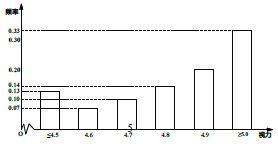
(1)求该校高一年级轻度近视患病率；
(2)根据保护视力的需要，需通知检查结果为“重度近视”学生的家长带孩子去医院眼科进一步检查和确诊，并开展相应的矫治，则该校高一年级需通知的家长人数约为多少人？
(3)若某班级6名学生中有2人为视力正常，则从这6名学生中任选2人，恰有1人视力正常的概率是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知：①函数
；
②向量
，
，且ω＞0，
；
③函数
的图象经过点
请在上述三个条件中任选一个，补充在下面问题中，并解答.
已知 ，且函数f（x）的图象相邻两条对称轴之间的距离为
.
（1）若
，且
，求f（θ）的值；
（2）求函数f（x）在[0，2π]上的单调递减区间.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某单位45名职工中随机抽取5名职工参加一项社区服务活动，用随机数法确定这5名职工
现将随机数表摘录部分如下：
从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字，则选出的第5个职工的编号为
A.23B.37C.35D.17
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥P-ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD=2，
E、F分别为CD、PB的中点．
（1）求证：EF⊥平面PAB；
（2）设
，求直线AC与平面AEF所成角θ的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，点
，圆
，点
是圆上一动点，线段
的中垂线与线段
交于点
.
（1）求动点
的轨迹
的方程；
（2）若直线
与曲线
相交于
两点，且存在点
（其中
不共线），使得
被
轴平分，证明：直线
过定点.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某电动车售后服务调研小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程（单次充电后能行驶的最大里程），被调查汽车的续驶里程全部介于50公里和300公里之间，将统计结果分成5组：
，绘制成如图所示的频率分布直方图.
（1）求续驶里程在
的车辆数；
（2）求续驶里程的平均数；
（3）若从续驶里程在的车辆中随机抽取2辆车，求其中恰有一辆车的续驶里程在
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
