
【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下: 表1:男生表2:女生
等级 | 优秀 | 合格 | 尚待改进 | 等级 | 优秀 | 合格 | 尚待改进 | |
频数 | 15 | x | 5 | 频数 | 15 | 3 | y |
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
男生 | 女生 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
参考数据与公式:
K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:
P(K2>k0) | 0.05 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
【答案】
(1)解:设从高一年级男生中抽出m人,则 ![]() =
= ![]() ,m=25,
,m=25,
∴x=25﹣20=5,y=20﹣18=2,
表2中非优秀学生共5人,记测评等级为合格的3人为a,b,c,尚待改进的2人为A,B,
则从这5人中任选2人的所有可能结果为:(a,b)(a,c)(b,c)(A,B)(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共10种.
设事件C表示“从表二的非优秀学生5人中随机选取2人,恰有1人测评等级为合格”,
则C的结果为:(a,A),(a,B),(b,A)(,b,B),(c,A)(c,B),共6种.
∴P(C)= ![]() =
= ![]() ,故所求概率为
,故所求概率为 ![]() .
.
男生 | 女生 | 总计 | |
优秀 | 15 | 15 | 30 |
非优秀 | 10 | 5 | 15 |
总计 | 25 | 20 | 45 |
(2)解:∵1﹣0.9=0.1,p(k2>2.706)=0.10,
而K2= ![]() =
= ![]() =
= ![]() =1.125<2.706,
=1.125<2.706,
所以没有90%的把握认为“测评结果优秀与性别有关”.
思路点拨(1)由题意可得非优秀学生共5人,记测评等级为合格的3人为a,b,c,尚待改进的2人为A,B,则从这5人中任选2人的所有可能结果为10个,设事件C表示“从表二的非优秀学生5人中随机选取2人,恰有1人测评等级为合格”,则C的结果为6个,根据概率公式即可求解.(2)由2×2列联表直接求解即可
【解析】(1)由题意可得非优秀学生共5人,记测评等级为合格的3人为a,b,c,尚待改进的2人为A,B,则从这5人中任选2人的所有可能结果为10个,设事件C表示“从表二的非优秀学生5人中随机选取2人,恰有1人测评等级为合格”,则C的结果为6个,根据概率公式即可求解.(2)由2×2列联表直接求解即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x2﹣ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若p∧q是真命题,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的参数方程为  (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4cosθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=4cosθ.
(1)把曲线C的极坐标方程化为直角坐标方程;
(2)设直线l与曲线C交于M,N两点,点A(1,0),求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1 , 抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上各取两个点,其坐标分别是(3,一2 ![]() ),(一2,0),(4,一4),(
),(一2,0),(4,一4),( ![]() ). (Ⅰ)求C1 , C2的标准方程;
). (Ⅰ)求C1 , C2的标准方程;
(Ⅱ)是否存在直线L满足条件:①过C2的焦点F;②与C1交与不同的两点M,N且满足 ![]() ?若存在,求出直线方程;若不存在,说明理由.
?若存在,求出直线方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
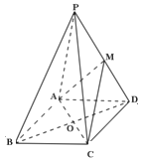
【题目】如图,已知在正四棱锥![]() 中,
中, ![]() 为侧棱
为侧棱![]() 的中点, 连接
的中点, 连接![]() 相交于点
相交于点![]() 。
。
(1)证明: ![]() ;
;
(2)证明: ![]() ;
;
(3)设![]() ,若质点从点
,若质点从点![]() 沿平面
沿平面![]() 与平面
与平面![]() 的表 面运动到点
的表 面运动到点![]() 的最短路径恰好经过点
的最短路径恰好经过点![]() ,求正四棱锥
,求正四棱锥 ![]() 的体积。
的体积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的定义域为D,若存在闭区间
的定义域为D,若存在闭区间![]()
![]() ,使得函数
,使得函数![]() 同时满足:
同时满足:
(1)![]() 在
在![]() 内是单调函数;
内是单调函数;
(2)![]() 在
在![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为
为![]() 的“
的“![]() 倍值区间”.
倍值区间”.
下列函数中存在“3倍值区间”的有_____.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
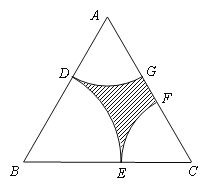
【题目】近年来,随着我市经济的快速发展,政府对民生也越来越关注. 市区现有一块近似正三角形土地ABC(如图所示),其边长为2百米,为了满足市民的休闲需求,市政府拟在三个顶点处分别修建扇形广场,即扇形DBE,DAG和ECF,其中![]() 、
、![]() 与
与![]() 分别相切于点D、E,且
分别相切于点D、E,且![]() 与
与![]() 无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
无重叠,剩余部分(阴影部分)种植草坪. 设BD长为x(单位:百米),草坪面积为S(单位:百米2).
(1)试用x分别表示扇形DAG和DBE的面积,并写出x的取值范围;
(2)当x为何值时,草坪面积最大?并求出最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com