圆x2+y2+x-6y+3=0上两点P、Q满足 ①关于直线kx-y+4=0对称,②OP⊥OQ.
(1)求k值;
(2)求直线PQ的方程.
解:(1)曲线x
2+y
2+x-6y+3=0可变为:
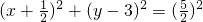
得到圆心(-

,3),半径为

;
因为圆上有两点P、Q关于直线对称,得到圆心在直线上,
把(-

,3)代入到kx-y+4=0中求出k=2
(2)直线PQ的斜率=
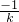
=-

;设PQ方程为
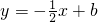
联立得
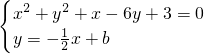
,代入整理得
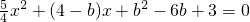
设P(x
1,y
1),Q(x
2,y
2),
∵OP⊥OQ.∴x
1x
2+y
1y
2=0
∴
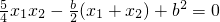
∴
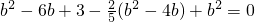
∴
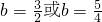
所以直线PQ的方程为:
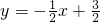
或
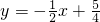
,经验证符合题意.
分析:(1)因为曲线方程为圆的方程,圆上的P与Q关于直线对称得到直线过圆心,把圆心坐标代入即可求出k;
(2)又因为PQ⊥直线kx-y+4=0得到直线PQ的斜率为
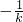
,然后联立直线与圆的方程,利用OP⊥OQ.∴x
1x
2+y
1y
2=0,再借助于韦达定理,即可写出直线的方程.
点评:本题的考点是关于点、直线对称的圆的方程,主要考查考查学生理解圆的对称轴为过直径的直线,会根据两直线垂直得到斜率乘积为-1,会根据条件写出直线的一般式方程.注意条件的等价转化.

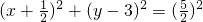
 ,3),半径为
,3),半径为 ;
; ,3)代入到kx-y+4=0中求出k=2
,3)代入到kx-y+4=0中求出k=2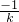 =-
=- ;设PQ方程为
;设PQ方程为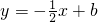
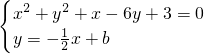 ,代入整理得
,代入整理得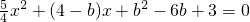
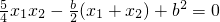
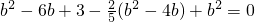
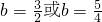
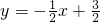 或
或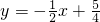 ,经验证符合题意.
,经验证符合题意.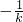 ,然后联立直线与圆的方程,利用OP⊥OQ.∴x1x2+y1y2=0,再借助于韦达定理,即可写出直线的方程.
,然后联立直线与圆的方程,利用OP⊥OQ.∴x1x2+y1y2=0,再借助于韦达定理,即可写出直线的方程.
