
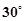 方向,距离A处
方向,距离A处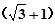 n mile的B处有一艘走私船
n mile的B处有一艘走私船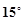 的方向,距离A处
的方向,距离A处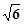 n mile的C处的缉私船奉命以
n mile的C处的缉私船奉命以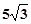 n mile/h的速度追截走私船. 此时,走私船正以5 n mile/h的速度从B处按照北偏东
n mile/h的速度追截走私船. 此时,走私船正以5 n mile/h的速度从B处按照北偏东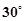 方向逃窜,问缉私船至少经过多长时间可以追上走私船,并指出缉私船航行方向.
方向逃窜,问缉私船至少经过多长时间可以追上走私船,并指出缉私船航行方向. 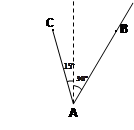
 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com