
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | -$\frac{3}{5}$ | D. | $\frac{3}{5}$ |
分析 利用两角和的正弦公式、诱导公式求得sin(α+$\frac{7π}{6}}$)的值.
解答 解:∵cos(α-$\frac{π}{6}}$)+sinα=$\frac{\sqrt{3}}{2}$cosα+$\frac{3}{2}$sinα=$\sqrt{3}$sin(α+$\frac{π}{6}$)=$\frac{4}{5}\sqrt{3}$,
∴sin(α+$\frac{π}{6}$)=$\frac{4}{5}$,
则sin(α+$\frac{7π}{6}}$)=-sin(α+$\frac{π}{6}$)=-$\frac{4}{5}$,
故选:B.
点评 本题主要考查两角和的正弦公式、诱导公式的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
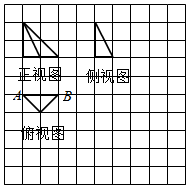 如图,网格上小正方形的边长为1,粗线画出的是一个三棱锥的三视图,该三棱锥的外接球的表面积记为S1,俯视图绕底边AB所在直线旋转一周形成的几何体的表面积记为S2,则S1:S2=( )
如图,网格上小正方形的边长为1,粗线画出的是一个三棱锥的三视图,该三棱锥的外接球的表面积记为S1,俯视图绕底边AB所在直线旋转一周形成的几何体的表面积记为S2,则S1:S2=( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | $\frac{1}{a-b}$>$\frac{1}{a}$ | C. | ac>bc | D. | a2<b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ”loga(x•y)=logax+logay“类比推出“sin(x•y)=sinx+siny“ | |
| B. | “(a+b)•c=ac+bc”类比推出“(a•b)•c=ac•bc” | |
| C. | “(a+b)•c=ac+bc”类比推出“$\frac{a+b}{c}$=$\frac{a}{c}+\frac{b}{c}$(c≠0)“ | |
| D. | “(a•b)•c=a•(b•c)“类比推出“($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)“ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com