
”¾ĢāÄæ”æij»Æ¹¤³§ŌŚ¶ØĘŚ¼ģŠŽÉč±øŹ±·¢ĻÖÉś²ś¹ÜµĄÖŠ¹²ÓŠ5“¦·§ĆÅ£Ø![]() £©·¢ÉśÓŠŗ¦ĘųĢ効Ā©.Ć擦·§ĆÅŌŚĆ抔Ź±ÄŚÓŠŗ¦ĘųĢåµÄŠ¹Ā¶Įæ“óĢåĻąµČ£¬Ō¼ĪŖ0.01Į¢·½Ć×.·§ĆŵĊŽø“¹¤×÷æÉŌŚ²»Ķ£²śµÄĒéæöĻĀŹµŹ©.ÓÉÓŚø÷·§ĆÅĖł“¦µÄĪ»ÖĆ²»Ķ¬£¬Ņņ“ĖŠŽø“ĖłŠčµÄŹ±¼ä²»Ķ¬£¬ĒŅŠŽø“Ź±±ŲŠė×ń“ÓŅ»¶ØµÄĖ³Šņ¹ŲĻµ£¬¾ßĢåĒéæöČēĻĀ±ķ£ŗ
£©·¢ÉśÓŠŗ¦ĘųĢ効Ā©.Ć擦·§ĆÅŌŚĆ抔Ź±ÄŚÓŠŗ¦ĘųĢåµÄŠ¹Ā¶Įæ“óĢåĻąµČ£¬Ō¼ĪŖ0.01Į¢·½Ć×.·§ĆŵĊŽø“¹¤×÷æÉŌŚ²»Ķ£²śµÄĒéæöĻĀŹµŹ©.ÓÉÓŚø÷·§ĆÅĖł“¦µÄĪ»ÖĆ²»Ķ¬£¬Ņņ“ĖŠŽø“ĖłŠčµÄŹ±¼ä²»Ķ¬£¬ĒŅŠŽø“Ź±±ŲŠė×ń“ÓŅ»¶ØµÄĖ³Šņ¹ŲĻµ£¬¾ßĢåĒéæöČēĻĀ±ķ£ŗ
Š¹Ā¶·§ĆÅ |
|
|
|
|
|
ŠŽø“Ź±¼ä £ØŠ”Ź±£© | 11 | 8 | 5 | 9 | 6 |
ŠčĻČŠŽø“ ŗƵķ§ĆÅ |
|
|
|
|
|
ŌŚÖ»ÓŠŅ»øö·§ĆÅŠŽø“Éč±øµÄĒéæöĻĀ£¬ŗĻĄķ°²ÅÅŠŽø“Ė³Šņ£¬Š¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”ĪŖ£Ø £©
A.1.14Į¢·½Ć×B.1.07Į¢·½Ć×C.1.04Į¢·½Ć×D.0.39Į¢·½Ć×
”¾“š°ø”æC
”¾½āĪö”æ
ĻČČ·¶ØÓŠŅŖĒóČżøö·§ĆÅ![]() µÄĻČŗóĖ³Šņ±ŲŠėŹĒ
µÄĻČŗóĖ³Šņ±ŲŠėŹĒ![]() £¬ŅŖŹ¹Š¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”£¬ŠŽø“Ź±¼ä³¤µÄŅņ¾”Įæææŗó£¬Č·¶ØŠŽø“Ė³ŠņĪŖ
£¬ŅŖŹ¹Š¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”£¬ŠŽø“Ź±¼ä³¤µÄŅņ¾”Įæææŗó£¬Č·¶ØŠŽø“Ė³ŠņĪŖ![]() £¬Č»ŗó¼ĘĖćĆæøö·§ĆÅŠ¹Ā¶ÓŠŗ¦ĘųĢåµÄŹ±¼ä£¬¼ĘĖć³öŠ¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”Öµ.
£¬Č»ŗó¼ĘĖćĆæøö·§ĆÅŠ¹Ā¶ÓŠŗ¦ĘųĢåµÄŹ±¼ä£¬¼ĘĖć³öŠ¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”Öµ.
ÓɱķÖŖ£¬øł¾ŻŠčĻČŠŽø“ŗƵķ§ĆŵÄŅŖĒó£¬æÉČ·¶Ø![]() Ė³ŠņĪŽŅŖĒó£¬ĘäÖŠČżøö·§ĆŵÄĻČŗóĖ³Šņ±ŲŠėŹĒ
Ė³ŠņĪŽŅŖĒó£¬ĘäÖŠČżøö·§ĆŵÄĻČŗóĖ³Šņ±ŲŠėŹĒ![]() £¬ŅŖŹ¹Š¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”£¬ŠŽø“Ź±¼ä³¤µÄŅņ¾”Įæææŗó£¬
£¬ŅŖŹ¹Š¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”£¬ŠŽø“Ź±¼ä³¤µÄŅņ¾”Įæææŗó£¬
¹ŹŠŽø“Ė³ŠņĪŖ![]() £¬
£¬
Ōņ![]() ø÷·§ĆÅŠ¹Ā¶ÓŠŗ¦ĘųĢåµÄŹ±¼ä·Ö±šĪŖ
ø÷·§ĆÅŠ¹Ā¶ÓŠŗ¦ĘųĢåµÄŹ±¼ä·Ö±šĪŖ![]() Š”Ź±£¬
Š”Ź±£¬
Š¹Ā¶ÓŠŗ¦ĘųĢåµÄŹ±¼ä¹²![]() Š”Ź±£¬
Š”Ź±£¬
¹ŹŠ¹Ā¶µÄÓŠŗ¦ĘųĢå×ÜĮæ×īŠ”ĪŖ![]() Į¢·½Ć×£¬
Į¢·½Ć×£¬
¹ŹŃ”£ŗC



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖa£¬b£¬c¾łĪŖÕżŹż£¬ÉčŗÆŹżf£Øx£©£½|x©b|©|x+c|+a£¬x”ŹR£®
£Ø1£©Čōa£½2b£½2c£½2£¬Ēó²»µČŹ½f£Øx£©£¼3µÄ½ā¼Æ£»
£Ø2£©ČōŗÆŹżf£Øx£©µÄ×ī“óÖµĪŖ1£¬Ö¤Ć÷£ŗ![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾Š”Ģā14·Ö£©ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĒśĻßC1µÄ²ĪŹż·½³ĢĪŖ![]() £Øa£¾b£¾0£¬
£Øa£¾b£¾0£¬![]() ĪŖ²ĪŹż£©£¬ŅŌ¦ÆĪŖ¼«µć£¬xÖįµÄÕż°ėÖįĪŖ¼«Öį½ØĮ¢¼«×ų±źĻµ£¬ĒśĻßC2ŹĒŌ²ŠÄŌŚ¼«ÖįÉĻĒŅ¾¹ż¼«µćµÄŌ²£¬ŅŃÖŖĒśĻßC1ÉĻµÄµć
ĪŖ²ĪŹż£©£¬ŅŌ¦ÆĪŖ¼«µć£¬xÖįµÄÕż°ėÖįĪŖ¼«Öį½ØĮ¢¼«×ų±źĻµ£¬ĒśĻßC2ŹĒŌ²ŠÄŌŚ¼«ÖįÉĻĒŅ¾¹ż¼«µćµÄŌ²£¬ŅŃÖŖĒśĻßC1ÉĻµÄµć![]() ¶ŌÓ¦µÄ²ĪŹż
¶ŌÓ¦µÄ²ĪŹż![]() £®
£®![]() ÓėĒśĻßC2½»ÓŚµć
ÓėĒśĻßC2½»ÓŚµć![]() £®
£®
£Ø1£©ĒóĒśĻßC1£¬C2µÄÖ±½Ē×ų±ź·½³Ģ£»
£Ø2£©![]() £¬
£¬![]() ŹĒĒśĻßC1ÉĻµÄĮ½µć£¬Ēó
ŹĒĒśĻßC1ÉĻµÄĮ½µć£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹż![]() £¬
£¬![]() .
.
£Ø1£©µ±![]() Ź±£¬×ÜÓŠ
Ź±£¬×ÜÓŠ![]() £¬Ēó
£¬Ēó![]() µÄ×īŠ”Öµ£»
µÄ×īŠ”Öµ£»
£Ø2£©¶ŌÓŚ![]() ÖŠČĪŅā
ÖŠČĪŅā![]() ŗćÓŠ
ŗćÓŠ![]() £¬Ēó
£¬Ēó![]() µÄȔֵ·¶Ī§.
µÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖÄĄā׶![]() ÖŠ£¬
ÖŠ£¬![]() Ę½·Ö
Ę½·Ö![]() .
.![]() .
.![]() .
.
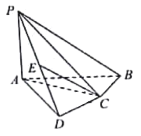
£Ø1£©ÉčEŹĒ![]() µÄÖŠµć£¬ĒóÖ¤£ŗ
µÄÖŠµć£¬ĒóÖ¤£ŗ![]() Ę½Ćę
Ę½Ćę![]() £»
£»
£Ø2£©Éč![]() Ę½Ćę
Ę½Ćę![]() £¬Čō
£¬Čō![]() ÓėĘ½Ćę
ÓėĘ½Ćę![]() Ėł³ÉµÄ½ĒĪŖ45”ć£¬Ēó¶žĆę½Ē
Ėł³ÉµÄ½ĒĪŖ45”ć£¬Ēó¶žĆę½Ē![]() µÄÓąĻŅÖµ.
µÄÓąĻŅÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
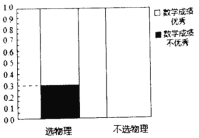
”¾ĢāÄæ”æijĘū³µÖĘŌģ³§ÖĘŌģĮĖijæīĘū³µ.ĪŖĮĖĮĖ½āĘū³µµÄŹ¹ÓĆĒéæö£¬ĶعżĪŹ¾ķµÄŠĪŹ½£¬Ė껜¶Ō50ĆūæĶ»§¶ŌøĆæīĘū³µµÄĻ²°®Ēéæö½ųŠŠµ÷²é£¬ČēĶ¼1ŹĒĘū³µŹ¹ÓĆÄźĻŽµÄµ÷²éʵĀŹ·Ö²¼Ö±·½Ķ¼£¬Čē±ķ2ŹĒøĆ50ĆūæĶ»§¶ŌĘū³µµÄĻ²°®Ēéæö.
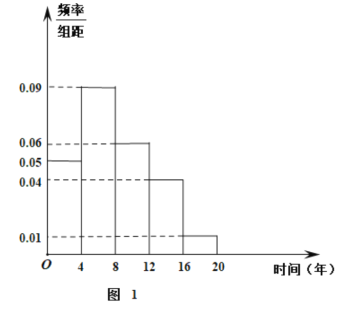
±ķ2
²»Ļ²»¶øĆæīĘū³µ | Ļ²»¶øĆæīĘū³µ | ×Ü¼Ę | |
Å®Źæ | 11 | ||
ÄŠŹæ | 23 | 30 | |
×Ü¼Ę |
£Ø1£©½«±ķ2²¹³äĶźÕū£¬²¢ÅŠ¶ĻÄÜ·ńŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż0.025µÄĒ°ĢįĻĀČĻĪŖŹĒ·ńĻ²»¶øĆæīĘū³µÓėŠŌ±šÓŠ¹Ų£»
£Ø2£©øł¾ŻĶ¼ÖŠµÄŹż¾Ż£¬¼×Ėµ£ŗ”°ÖŠĪ»ŹżŌŚ![]() ×éÄŚ”±£»ŅŅĖµ£ŗ”°Ę½¾łŹż“óÓŚÖŠĪ»Źż”±£»±ūĖµ£ŗ”°ÖŠĪ»ŹżŗĶĘ½¾łŹżŅ»Ńł”±£¬Õė¶ŌČżĪ»Ķ¬Ń§µÄĖµ·Ø£¬ÄćČĻĪŖÄÄÖÖĖµ·ØŗĻĄķ£¬øų³öĖµĆ÷.
×éÄŚ”±£»ŅŅĖµ£ŗ”°Ę½¾łŹż“óÓŚÖŠĪ»Źż”±£»±ūĖµ£ŗ”°ÖŠĪ»ŹżŗĶĘ½¾łŹżŅ»Ńł”±£¬Õė¶ŌČżĪ»Ķ¬Ń§µÄĖµ·Ø£¬ÄćČĻĪŖÄÄÖÖĖµ·ØŗĻĄķ£¬øų³öĖµĆ÷.
ø½£ŗ![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÖ±Ļß![]() ÓėÅ×ĪļĻß
ÓėÅ×ĪļĻß![]() Ļą½»ÓŚA£¬BĮ½µć£¬ĒŅÓėŌ²
Ļą½»ÓŚA£¬BĮ½µć£¬ĒŅÓėŌ²![]() ĻąĒŠ.
ĻąĒŠ.
£Ø1£©ĒóÖ±Ļß![]() ŌŚxÖįÉĻ½Ų¾ą
ŌŚxÖįÉĻ½Ų¾ą![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
£Ø2£©ÉčFŹĒÅ×ĪļĻߵĽ¹µć£¬![]() £¬ĒóÖ±Ļß
£¬ĒóÖ±Ļß![]() µÄ·½³Ģ.
µÄ·½³Ģ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹ”¼“½«ŹµŠŠŠĀøßæ¼£¬²»ŌŁŹµŠŠĪÄĄķ·ÖæĘ.ijŠ£ĪŖĮĖŃŠ¾æŹżŃ§³É¼ØÓÅŠćŹĒ·ń¶ŌŃ”ŌńĪļĄķÓŠÓ°Ļģ£¬¶ŌøĆŠ£2018¼¶µÄ1000Ćūѧɜ½ųŠŠµ÷²é£¬ŹÕ¼Æµ½Ļą¹ŲŹż¾ŻČēĻĀ£ŗ
£Ø1£©øł¾ŻŅŌÉĻĢį¹©µÄŠÅĻ¢£¬Ķź³É![]() ĮŠĮŖ±ķ£¬²¢ĶźÉʵČøßĢõŠĪĶ¼£»
ĮŠĮŖ±ķ£¬²¢ĶźÉʵČøßĢõŠĪĶ¼£»
Ń”ĪļĄķ | ²»Ń”ĪļĄķ | ×Ü¼Ę | |
ŹżŃ§³É¼ØÓÅŠć | |||
ŹżŃ§³É¼Ø²»ÓÅŠć | 260 | ||
×Ü¼Ę | 600 | 1000 |
£Ø2£©ÄÜ·ńŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż0.05µÄĒ°ĢįĻĀČĻĪŖŹżŃ§³É¼ØÓÅŠćÓėŃ”ĪļĄķÓŠ¹Ų£æ
ø½£ŗ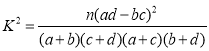
ĮŁ½ēÖµ±ķ£ŗ
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠÓŠ¹ŲĻߊŌ»Ų¹é·ÖĪöµÄĖÄøöĆüĢā£ŗ
¢ŁĻߊŌ»Ų¹éÖ±Ļß±Ų¹żŃł±¾Źż¾ŻµÄÖŠŠÄµć£Ø![]() £©£»
£©£»
¢Ś»Ų¹éÖ±Ļß¾ĶŹĒÉ¢µćĶ¼ÖŠ¾¹żŃł±¾Źż¾Żµć×ī¶ąµÄÄĒĢõÖ±Ļߣ»
¢Ūµ±Ļą¹ŲŠŌĻµŹż![]() Ź±£¬Į½øö±äĮæÕżĻą¹Ų£»
Ź±£¬Į½øö±äĮæÕżĻą¹Ų£»
¢ÜČē¹ūĮ½øö±äĮæµÄĻą¹ŲŠŌŌ½Ē棬ŌņĻą¹ŲŠŌĻµŹż![]() ¾ĶŌ½½Ó½üÓŚ
¾ĶŌ½½Ó½üÓŚ![]() £®
£®
ĘäÖŠÕęĆüĢāµÄøöŹżĪŖ£Ø””””£©
A. 1øö B. 2øö C. 3øö D. 4øö
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com