
【题目】已知抛物线y2=2px(p>0)上一点P(3,t)到其焦点的距离为4.
(1)求p的值;
(2)过点Q(1,0)作两条直线l1 , l2与抛物线分别交于点A、B和C、D,点M,N分别是线段AB和CD的中点,设直线l1 , l2的斜率分别为k1 , k2 , 若k1+k2=3,求证:直线MN过定点.
【答案】解:(1)抛物线y2=2px的焦点为(![]() ,0),准线为x=﹣
,0),准线为x=﹣![]() ,
,
由抛物线的定义可得,3+![]() =4,解得p=2;
=4,解得p=2;
(2)证明:由题意知,k1+k2=3,
不妨设AB的斜率k1=k,则CD的斜率k2=3﹣k,
所以AB的直线方程是:y=k(x﹣1),CD的直线方程是y=(3﹣k)(x﹣1),
设A(x1 , y1),B(x2 , y2),
由 ![]() ,得,k2x2﹣(2k2+4)x+k2=0,
,得,k2x2﹣(2k2+4)x+k2=0,
则x1+x2=![]() ,x1x2=1,
,x1x2=1,
所以y1+y2=k(x1﹣1)+k(x2﹣1)=k(2+![]() )﹣2k=
)﹣2k=![]() ,
,
因为M是AB的中点,所以点M(1+![]() ,
,![]() ),
),
同理可得,点N(1+![]() ,
,![]() ),
),
所以直线MN的方程是:y﹣![]() =
=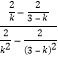 (x﹣1﹣
(x﹣1﹣![]() ),
),
化简得,y=(k﹣k2)(x﹣1)+![]() ,令x=1,得y=
,令x=1,得y=![]() ,
,
所以直线MN过定点(1,![]() ).
).
【解析】(1)求得抛物线的焦点和准线方程,运用抛物线的定义,可得p=2;
(2)不妨设AB的斜率k1=k,求出CD的斜率k2=3﹣k,利用点斜式方程求出直线AB、CD的方程,与抛物线方程联立消x得关于y的一元二次方程,根据韦达定理即可求得中点M、N的坐标,利用点斜式方程求出直线MN的方程,化简后求出直线MN经过的定点坐标.


科目:高中数学 来源: 题型:
【题目】在独立性检验中,统计量![]() 有三个临界值:2.706,3.841和6.635.当
有三个临界值:2.706,3.841和6.635.当![]() 时,有90%的把握说明两个事件有关;当
时,有90%的把握说明两个事件有关;当![]() 时,有95%的把握说明两个事件有关,当
时,有95%的把握说明两个事件有关,当![]() 时,有99%的把握说明两个事件有关,当
时,有99%的把握说明两个事件有关,当![]() 时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算
时,认为两个事件无关.在一项打鼾与心脏病的调查中,共调查了2000人,经计算![]() .根据这一数据分析,认为打鼾与患心脏病之间( )
.根据这一数据分析,认为打鼾与患心脏病之间( )
A. 有95%的把握认为两者有关 B. 约95%的打鼾者患心脏病
C. 有99%的把握认为两者有关 D. 约99%的打鼾者患心脏病
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+![]() , g(x)=x+lnx,其中a>0,且x∈(0,+∞).
, g(x)=x+lnx,其中a>0,且x∈(0,+∞).
(1)若a=1,求f(x)的最小值;
(2)若对任意x≥1,不等式f(x)≤g(x)恒成立,求实数a的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱ABCD-A1B1C1D1中,![]() ,平面BB1C1C
,平面BB1C1C![]() 底面ABCD,点
底面ABCD,点![]() 、F分别是线段
、F分别是线段![]() 、BC的中点.
、BC的中点.
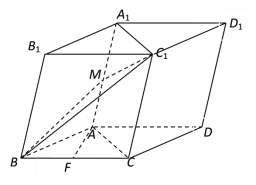
(1)求证:AF//平面![]() ;
;
(2)求证:平面BB1C1C⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①在线性回归模型中,相关指数![]() 表示解释变量
表示解释变量![]() 对于预报变量
对于预报变量![]() 的贡献率,
的贡献率, ![]() 越接近于1,表示回归效果越好;②两个变量相关性越强,则相关系数的绝对值就越接近于1;③在回归直线方程
越接近于1,表示回归效果越好;②两个变量相关性越强,则相关系数的绝对值就越接近于1;③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;④对分类变量
平均减少0.5个单位;④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.其中正确命题的个数是( )
有关系”的把握程度越大.其中正确命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年10月19日,由中国工信部、江西省政府联合主办的世界VR(虚拟现实)产业大会在南昌开幕,南昌在红谷滩新区建立VR特色小镇项目.现某厂商抓住商机在去年用450万元购进一批VR设备,经调试后今年投入使用,计划第一年维修、保养费用22万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该设备使用后,每年的总收入为180万元,设使用x年后设备的盈利额为y万元.
(1)写出y与x之间的函数关系式;
(2)使用若干年后,当年平均盈利额达到最大值时,求该厂商的盈利额.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最大值为60°.
其中正确的是________.(填写所有正确结论的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com