
【题目】已知函数f(x)=|x2﹣1|+x2+kx.
(1)若对于区间(0,+∞)内的任意x,总有f(x)≥0成立,求实数k的取值范围;
(2)若函数f(x)在区间(0,2)内有两个不同的零点x1 , x2 , 求:
①实数k的取值范围;
② ![]() 的取值范围.
的取值范围.
【答案】
(1)解:f(x)≥0|x2﹣1|+x2+kx≥0k≥﹣ ![]() ,x∈(0,+∞),
,x∈(0,+∞),
记g(x)=﹣ ![]() =
= 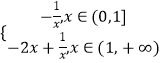 ,易知g(x)在(0,1]上递增,在(1,+∞)上递减,
,易知g(x)在(0,1]上递增,在(1,+∞)上递减,
∴g(x)max=g(1)=﹣1,
∴k≥﹣1;
(2)解:①(ⅰ)0<x≤1时,方程f(x)=0化为kx+1=0,k=0时,无解;k≠0时,x=﹣ ![]() ;
;
(ⅱ)1<x<2时,方程f(x)=0化为2x2+kx﹣1=0,x= ![]() ,而其中
,而其中 ![]() <
< ![]() ≤0,
≤0,
故f(x)=0在区间(1,2)内至多有一解x= ![]() ;
;
综合(ⅰ)(ⅱ)可知,k≠0,且0<x≤1时,方程f(x)=0有一解x=﹣ ![]() ,故k≤﹣1;
,故k≤﹣1;
1<x<2时,方程f(x)=0也仅有一解x= ![]() ,令1<
,令1< ![]() <2,得﹣
<2,得﹣ ![]() <k<﹣1,
<k<﹣1,
∴实数k的取值范围是﹣ ![]() <k<﹣1;
<k<﹣1;
②方程f(x)=0的两解分别为x1=﹣ ![]() ,x2=
,x2= ![]() ,
,
![]() =﹣k+
=﹣k+ ![]() =﹣k+
=﹣k+ ![]() =
= ![]() =2x2∈(2,4).
=2x2∈(2,4).
【解析】(1)由f(x)≥0分离出参数k,得k≥﹣ ![]() ,x∈(0,+∞),记g(x)=﹣
,x∈(0,+∞),记g(x)=﹣ ![]() ,则问题等价于k≥g(x)max , 由单调性可得g(x)max;(2)①(i)当0<x≤1时,方程f(x)=0为一次型方程,易判断k≠0时有一解;当1<x<2时,方程f(x)=0为二次方程,可求得两解,易判断其一不适合,令另一解大于1小于2,可得k的范围,综合可得结论;(ii)由①易知两零点x1 , x2 , 从而可表示出
,则问题等价于k≥g(x)max , 由单调性可得g(x)max;(2)①(i)当0<x≤1时,方程f(x)=0为一次型方程,易判断k≠0时有一解;当1<x<2时,方程f(x)=0为二次方程,可求得两解,易判断其一不适合,令另一解大于1小于2,可得k的范围,综合可得结论;(ii)由①易知两零点x1 , x2 , 从而可表示出 ![]() ,化简可得为2x2 , 结合(ii)可得结论;
,化简可得为2x2 , 结合(ii)可得结论;


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
(1)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(2)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为 ![]() ,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量X表示这3人中通过预选赛的人数,求X的分布列与数学期望.
附:K2= ![]()
P(K2≥k) | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+bx+c(其中b,c为实常数).
(1)若b>2,且y=f(sinx)(x∈R)的最大值为5,最小值为﹣1,求函数y=f(x)的解析式;
(2)是否存在这样的函数y=f(x),使得{y|y=x2+bx+c,﹣1≤x≤0}=[﹣1,0],若存在,求出函数y=f(x)的解析式;若不存在,请说明理由.
(3)记集合A={x|f(x)=x,x∈R},B={x|f(f(x))=x,x∈R}.
①若A≠,求证:B≠;
②若A=,判断B是否也为空集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【扬州市2016—2017学年度第一学期期末检测】(本小题满分14分)
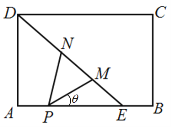
如图,矩形ABCD是一个历史文物展览厅的俯视图,点E在AB上,在梯形BCDE区域内部展示文物,DE是玻璃幕墙,游客只能在![]() ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,
ADE区域内参观.在AE上点P处安装一可旋转的监控摄像头,![]() 为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,
为监控角,其中M、N在线段DE(含端点)上,且点M在点N的右下方.经测量得知:AD=6米,AE=6米,AP=2米,![]() .记
.记![]() (弧度),监控摄像头的可视区域
(弧度),监控摄像头的可视区域![]() PMN的面积为S平方米.
PMN的面积为S平方米.
(1)求S关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;(参考数据:
的取值范围;(参考数据:![]() )
)
(2)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100mL(不含80)之间,属于酒后驾车;在80mg/100mL(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如表:
酒精含量(mg/100mL) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
(1)绘制出检测数据的频率分布直方图(计算并标上选取的y轴单位长度,在图中用实线画出矩形框并用阴影表示),估计检测数据中酒精含量的众数
(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的中位数、平均数(请写出计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
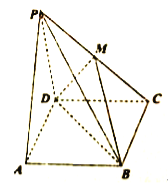
【题目】【2017辽宁庄河市四模】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)点![]() 在
在![]() 上,且满足
上,且满足![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
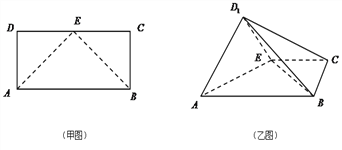
【题目】【2017四川宜宾二诊】如甲图所示,在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 位置,使平面
位置,使平面![]() 平面
平面![]() ,得到乙图所示的四棱锥
,得到乙图所示的四棱锥![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国谜语大会》是中央电视台科教频道的一档集文化、益智、娱乐为一体的大型电视竞猜节目,目的是为弘扬中国传统文化、丰富群众文化生活.为选拔选手参加“中国谜语大会”,某地区举行了一次“谜语大赛”活动.为了了解本次竞赛选手的成绩情况,从中抽取了部分选手的分数(得分取正整数,满分为100分)作为样本进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100)的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60),[90,100)的数据). 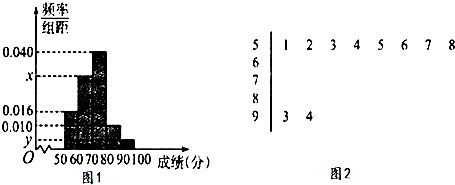
(1)求样本容量n和频率分布直方图中的x,y的值;
(2)分数在[80,90)的学生中,男生有2人,现从该组抽取三人“座谈”,求至少有两名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com