
【题目】已知函数![]()
![]() 的部分图象如图所示.
的部分图象如图所示.

(1)求![]() 与
与![]() 的值;
的值;
(2)设![]() 的三个角
的三个角![]() 、
、![]() 、
、![]() 所对的边依次为
所对的边依次为![]() 、
、![]() 、
、![]() ,如果
,如果![]() ,且
,且 ,试求
,试求![]() 的取值范围;
的取值范围;
(3)求函数![]()
![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 相交于
相交于![]() 两点.
两点.
(I)试写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某园林基地培育了一种新观赏植物,经过了一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为![]() )进行统计,按照[50,60),[60,70),[70,80),
)进行统计,按照[50,60),[60,70),[70,80),
[80,90),[90,100]分组做出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了
高度在[50,60),[90,100]的数据).
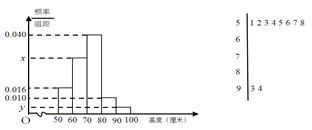
1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]()
2)在选取的样本中,从高度在80厘米以上(含80厘米)的植株中随机抽取3株,设随机变量![]() 表示所抽取的3株高度在 [80,90) 内的株数,求随机变量
表示所抽取的3株高度在 [80,90) 内的株数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知集合A={x|-2<x<0},B={x|y=![]() }
}
(1)求(RA)∩B;
(2)若集合C={x|a<x<2a+1}且CA,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13 s与19 s之间,将测试结果分成如下六组:[13,14),[14,15),[15,16),[16,17),[17,18),[18,19].如图是按上述分组方法得到的频率分布直方图,设成绩小于17 s的学生人数占全班人数的百分比为x,成绩在[15,17)中的学生人数为y,则从频率分布直方图中可以分析出x和y分别为 ( )
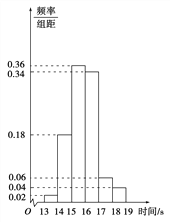
A. 90%,35B. 90%,45
C. 10%,35D. 10%,45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com