
【题目】已知函数![]() 的极小值为
的极小值为![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)证明:![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
【答案】(1)单调递减区间为 ,单调递增区间为
,单调递增区间为 (2)详见解析
(2)详见解析
【解析】
(1)先由函数![]() 的极小值为
的极小值为![]() ,求出
,求出![]() ,利用导数的应用,求函数单调区间即可;
,利用导数的应用,求函数单调区间即可;
(2)不等式恒成立问题,通常采用最值法,方法一,令![]() ,可以证明
,可以证明![]() ,方法二,要证
,方法二,要证![]() ,即证
,即证![]() ,再构造函数证明即可得解.
,再构造函数证明即可得解.
(1)由题得![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为 .
.
(2)方法一:要证![]() ,即证
,即证![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() 时
时![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() .
.
由题知![]() .
.
因为![]() ,
,
所以![]() ,即
,即![]() .
.
方法二:由(1)知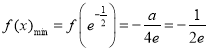 .
.
解得![]() ,要证
,要证![]() ,即证
,即证![]() .
.
当![]() 时,易知
时,易知![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
所以![]() ,即
,即![]() .
.
令![]() ,则
,则![]() ,
,
所以![]() 在区间
在区间![]() 内单调递增,
内单调递增,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
则当![]() 时,
时,![]()
![]() ,
,
所以![]() .
.
综上,![]() .
.


科目:高中数学 来源: 题型:
【题目】若对于定义在![]() 上的函数
上的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数
对任意实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() 特征函数”.下列结论中正确的个数为( )
特征函数”.下列结论中正确的个数为( )
①![]() 是常数函数中唯一的“
是常数函数中唯一的“![]() 特征函数”;
特征函数”;
②![]() 不是“
不是“![]() 特征函数”;
特征函数”;
③“![]() 特征函数”至少有一个零点;
特征函数”至少有一个零点;
④![]() 是一个“
是一个“![]() 特征函数”.
特征函数”.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列说法:
(1)命题“若![]() 、
、![]() 都是奇数,则
都是奇数,则![]() 是偶数”的否命题是“若
是偶数”的否命题是“若![]() 、
、![]() 都不是奇数,则
都不是奇数,则![]() 不是偶数”;
不是偶数”;
(2)命题“如果![]() ,那么
,那么![]() ”是真命题;
”是真命题;
(3)“![]() 或
或![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
那么其中正确的说法有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄金分割起源于公元前![]() 世纪古希腊的毕达哥拉斯学派,公元前
世纪古希腊的毕达哥拉斯学派,公元前![]() 世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,公元前
世纪,古希腊数学家欧多克索斯第一个系统研究了这一问题,公元前![]() 年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为
年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果,进一步系统论述了黄金分割,成为最早的有关黄金分割的论著.黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值为![]() ,把
,把![]() 称为黄金分割数. 已知双曲线
称为黄金分割数. 已知双曲线![]() 的实轴长与焦距的比值恰好是黄金分割数,则
的实轴长与焦距的比值恰好是黄金分割数,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程是
的参数方程是 (m>0,t为参数),曲线
(m>0,t为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学每年暑假举行“学科思维讲座”活动,每场讲座结束时,所有听讲者都要填写一份问卷调查.2017年暑假某一天五场讲座收到的问卷分数情况如下表:

用分层抽样的方法从这一天的所有问卷中抽取300份进行统计,结果如下表:

(1)估计这次讲座活动的总体满意率;
(2)求听数学讲座的甲某的调查问卷被选中的概率;
(3)若想从调查问卷被选中且填写不满意的人中再随机选出5人进行家访,求这5人中选择的是理综讲座的人数的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元,求:
(1)仓库顶部面积![]() 的最大允许值是多少?
的最大允许值是多少?
(2)为使![]() 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com