
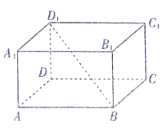
【题目】如图所示,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,过
,过![]() 的截面的面积为
的截面的面积为![]() ,则
,则![]() 的最小值为______.
的最小值为______.
【答案】![]()
【解析】
截面可能是矩形,可能是平行四边形;当截面是矩形时,矩形![]() 的面积最小;当截面是平行四边形时,可作出截面的三种不同状态,求得每种状态下截面面积的最小值后,即可确定总体最小值.
的面积最小;当截面是平行四边形时,可作出截面的三种不同状态,求得每种状态下截面面积的最小值后,即可确定总体最小值.
由题意可知:截面可能是矩形,可能是平行四边形.
(1)当截面为矩形时,即截面为![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,此时矩形
,此时矩形![]() 的面积最小;
的面积最小;
(2)当截面为平行四边形时,有三种位置:![]() ,
,![]() ,
,![]() ,如图所示,
,如图所示,


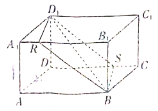
对于截面![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,如图(a)所示:
,如图(a)所示:

由对称性可知![]() ,
,![]() ,
,![]() ,
,
过点![]() 作
作![]() 交
交![]()
![]() .连接
.连接![]() ,当
,当![]() 时,
时,![]() 最小,此时
最小,此时![]() 的值最小.
的值最小.
![]() ,则四边形
,则四边形![]() 的面积的最小值为
的面积的最小值为![]() .
.
同理可得四边形![]() 的面积的最小值为
的面积的最小值为![]() ,
,
同理可得四边形![]() 的面积的最小值为
的面积的最小值为![]() ,
,
又因为![]() ,所以当截面为平行四边形时,截面面积最小值为
,所以当截面为平行四边形时,截面面积最小值为![]() .
.
又因为![]() ,所以过
,所以过![]() 的截面面积
的截面面积![]() 的最小值为
的最小值为![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】某工厂生产一种产品的标准长度为![]() ,只要误差的绝对值不超过
,只要误差的绝对值不超过![]() 就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
就认为合格,工厂质检部抽检了某批次产品1000件,检测其长度,绘制条形统计图如图:
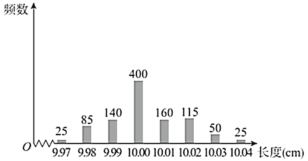
(1)估计该批次产品长度误差绝对值的数学期望;
(2)如果视该批次产品样本的频率为总体的概率,要求从工厂生产的产品中随机抽取2件,假设其中至少有1件是标准长度产品的概率不小于0.8时,该设备符合生产要求.现有设备是否符合此要求?若不符合此要求,求出符合要求时,生产一件产品为标准长度的概率的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的准线上一点,F为抛物线的焦点,P为抛物线上的点,且
的准线上一点,F为抛物线的焦点,P为抛物线上的点,且![]() ,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
,若双曲线C中心在原点,F是它的一个焦点,且过P点,当m取最小值时,双曲线C的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生鲜超市每天从蔬菜生产基地购进某种蔬菜,每天的进货量相同,进价6元/千克,售价9元/千克,当天未售出的蔬菜被生产基地以2元/千克的价格回收处理.该超市发现这种蔬菜每天都有剩余,为此整理了过往30天这种蔬菜的日需求量![]() (单位:千克),得到如下统计数据:
(单位:千克),得到如下统计数据:
日需求量 | 160 | 170 | 180 | 190 | 200 | 210 | 220 |
天数 | 3 | 6 | 6 | 9 | 4 | 1 | 1 |
以这30天记录的各日需求量的频率作为各日需求量的概率,假设各日需求量相互独立.
(1)求在未来的3天中,至多有1天的日需求量不超过190千克的概率;
(2)超市为了减少浪费,提升利润,决定调整每天的进货量![]() (单位:千克),以销售这种蔬菜的日利润的期望值为决策依据,在
(单位:千克),以销售这种蔬菜的日利润的期望值为决策依据,在![]() 与
与![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人进行乒乓球比赛,两人打到![]() 平,之后的比赛要每球交替发球权且要一人净胜两球才能取胜,已知甲发球甲获胜的概率为
平,之后的比赛要每球交替发球权且要一人净胜两球才能取胜,已知甲发球甲获胜的概率为![]() ,乙发球甲获胜的概率为
,乙发球甲获胜的概率为![]() ,则下列命题正确的个数为( )
,则下列命题正确的个数为( )
(1)若![]() ,两人能在两球后结束比赛的概率与
,两人能在两球后结束比赛的概率与![]() 有关
有关
(2)若![]() ,两人能在两球后结束比赛的概率与
,两人能在两球后结束比赛的概率与![]() 有关
有关
(3)第二球分出胜负的概率与在第二球没有分出胜负的情况下进而第四球分出胜负的概率相同
(4)第二球分出胜负的概率与在第![]() 球没有分出胜负的情况下进而第
球没有分出胜负的情况下进而第![]() 球分出胜负的概率相同
球分出胜负的概率相同
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
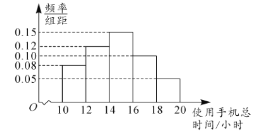
【题目】为了解学生课外使用手机的情况,某学校收集了本校500名学生2019年12月课余使用手机的总时间(单位:小时)的情况.从中随机抽取了50名学生,将数据进行整理,得到如图所示的频率分布直方图.已知这50名学生中,恰有3名女生课余使用手机的总时间在![]() ,现在从课余使用手机总时间在
,现在从课余使用手机总时间在![]() 的样本对应的学生中随机抽取3名,则至少抽到2名女生的概率为( )
的样本对应的学生中随机抽取3名,则至少抽到2名女生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com