
【题目】已知点![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,
,![]() 是椭圆
是椭圆![]() 的右焦点,直线
的右焦点,直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点. 设过点
为坐标原点. 设过点![]() 的动直线
的动直线![]() 与
与![]() 相交于
相交于![]() 两点.
两点.
(1)求![]() 的方程;
的方程;
(2)是否存在这样的直线![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在,求出
,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】记矩阵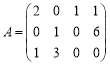 中的第
中的第![]() 行第
行第![]() 列上的元素为
列上的元素为![]() ,现对矩阵
,现对矩阵![]() 中的元素按如下算法所示的步骤作变动(直到不能变动为止):若
中的元素按如下算法所示的步骤作变动(直到不能变动为止):若![]() ,则
,则![]() ,
,![]() ,
,![]() ,若
,若![]() ,则不变动,这样得到矩阵B,再对矩阵B中的元素按如下算法所示的步骤作变动(直到不能变动为止):若
,则不变动,这样得到矩阵B,再对矩阵B中的元素按如下算法所示的步骤作变动(直到不能变动为止):若![]() ,则
,则![]() ,
,![]() ,
,![]() ;若
;若![]() ,则不变动,这样得到矩阵
,则不变动,这样得到矩阵![]() ,则
,则![]() ________;
________;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据阅兵领导小组办公室介绍,2019年国庆70周年阅兵有59个方(梯)队和联合军乐团,总规模约1.5万人,是近几次阅兵中规模最大的一次.其中,徒步方队15个.为了保证阅兵式时队列保持整齐,各个方队对受阅队员的身高也有着非常严格的限制,太高或太矮都不行.徒步方队队员,男性身高普遍在175cm至185cm之间;女性身高普遍在163cm至175cm之间,这是常规标准.要求最为严格的三军仪仗队,其队员的身高一般都在184cm至190cm之间.经过随机调查某个阅兵阵营中女子100人,得到她们身高的直方图,如图,记C为事件:“某一阅兵女子身高不低于169cm”,根据直方图得到P(C)的估计值为0.5.
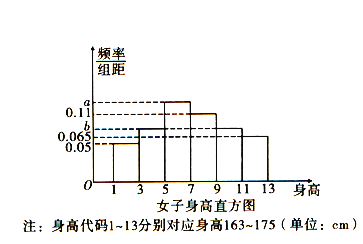
(1)求直方图中a,b的值;
(2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)求购买金额不少于45元的频率;
(2)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
女 | 18 | ||
合计 |
附:参考公式和数据: ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数,
是参数,![]() 是大于0的常数).以坐标原点为极点,
是大于0的常数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)分别记直线![]() :
:![]() ,
,![]() 与圆
与圆![]() 、圆
、圆![]() 的异于原点的交点为
的异于原点的交点为![]() ,
,![]() ,若圆
,若圆![]() 与圆
与圆![]() 外切,试求实数
外切,试求实数![]() 的值及线段
的值及线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学进行自主招生测试,需要对逻辑思维和阅读表达进行能力测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如图所示,下列叙述正确的是( )
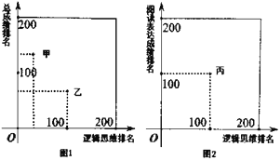
A.甲同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
B.乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
C.甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前
D.甲同学的总成绩排名比丙同学的总成绩排名更靠前
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com