
 ( p为常数),则称{an}为“等方差数列”.下列是对“等方差数列”的判断:
( p为常数),则称{an}为“等方差数列”.下列是对“等方差数列”的判断: 是等差数列;
是等差数列;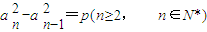 ,则数列
,则数列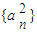 是公差为p的等差数列,所以(1)正确.
是公差为p的等差数列,所以(1)正确.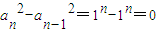 ,所以数列{(-1)n}是等方差数列,所以(2)正确.
,所以数列{(-1)n}是等方差数列,所以(2)正确. ,即(an-an-1)(an+an-1)=p,
,即(an-an-1)(an+an-1)=p,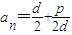 ,所以数列{an}是常数列,综上数列{an}是常数列,所以(3)正确.
,所以数列{an}是常数列,综上数列{an}是常数列,所以(3)正确.

科目:高中数学 来源: 题型:
| 5x-a | x+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| an |
| (y-1)2 |
| 4 |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省文登市高三上学期期中统考理科数学试卷(解析版) 题型:选择题
给出下列四个命题,其错误的是( )
①已知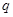 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 是递增数列”是“
是递增数列”是“ ”的既不充分也不必要条件;
”的既不充分也不必要条件;
②若定义在 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
;
③若存在正常数 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
;
④函数 与
与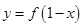 图像关于
图像关于 对称.
对称.
A.②④ B.④ C.③ D.③④
查看答案和解析>>
科目:高中数学 来源:2012届安徽省六校教育研究会高二素质测试理科数学 题型:填空题
给出下列命题:
①.在等差数列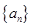 中
中 ,且
,且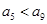 ,则使数列前n项和
,则使数列前n项和 取最小值的n等于5;
取最小值的n等于5;
②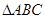 的外接圆的圆心为O,半径为1,
的外接圆的圆心为O,半径为1, ,且
,且 ,则向量
,则向量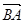
在向量 方向上的投影为
方向上的投影为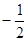 ;
;
③ 函数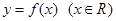 的值域是集合A,则函数
的值域是集合A,则函数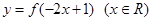 的值域也是集合A;
的值域也是集合A;
④直线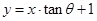 的倾斜角是
的倾斜角是 ;
;
⑤若定义在区间D上的函数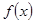 对于D上任意n个值
对于D上任意n个值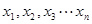 总满足
总满足 ,则
,则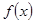 称为D上的凸函数,现已知
称为D上的凸函数,现已知
 上凸函数,则锐角三角形△ABC中
上凸函数,则锐角三角形△ABC中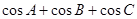 的最大值为
的最大值为
 。其中正确命题的序号是_______。
。其中正确命题的序号是_______。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com