Question

已知等差数列{a_n}的首项为a，公差为b；等比数列{b_n}的首项为b;公比为a，其中a，b∈N^*且a₁＜b₁＜a₂＜b₂＜a₃.

(Ⅰ)求a的值；

(Ⅱ)若对于任意n∈N^*，总存在m∈N^*使a_m+3=b_n，求b的值；

(Ⅲ)在(Ⅱ)中，记{c_n}是所有{a_n}中满足a_m+3=b_n，m∈N^*项从小到大依次组成的数列，又记S_n为{c_n}的前n项和，T_n为{a_n}的前n项和，求证：S_n≥T_n(n∈N^*).

Answer 1

解：(Ⅰ)∵a＜b＜a+b＜ab＜a+2b,a,b∈N⁺

∴∴

∴∴

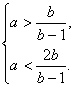
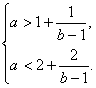∵ab＜a+2b＜3b  ∴a＜3  ∴a=2 

(Ⅱ)a_m=2+(m-1)b,b_n=b·2^n-1,由a_m+3=b_n可得5+(m-1)b=b·2^n-1,∴b(2^n-1-m+1)=5. 

∴b=5 

(Ⅲ)由(Ⅱ)知a_n=5n-3,b_n=5·2^n-1,2^n-1-m+1=1∴a_m=b_n-3=5·2^n-1-3. 

∴C_n=5·2^n-1,-3,∴S_n=5(2ⁿ-1)-3_n,T_n=n(5n-1).∵S₁=T₁=2,S₂=T₂=9. 

当n≥3时S_n-T_n=5[2ⁿ]

             =5[(1+1)ⁿn²n-1]

             =5[()] 

             ＞5[1+n+]=0.

∴S_n＞T_n.综上得S_n≥T_n(n∈N^*).